题目内容
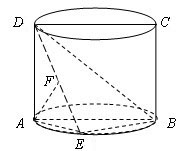
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π。
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求直线DE与平面ABCD所成角的正切值。
(Ⅰ)证明见解析。
(Ⅱ)![]()
解析:
(Ⅰ)因为AD⊥平面ABE,所以 AD⊥BE。
又AE⊥BE,AD∩AE=A,所以BE⊥平面ADE。 (3分)
因为AF![]() 平面ADE,所以BE⊥AF。
平面ADE,所以BE⊥AF。
又AF⊥DE,所以AF⊥平面BDE,故AF⊥BD。 (6分)
(Ⅱ)过点E作EO⊥AB,垂足为O。
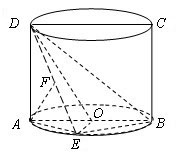
因为平面ABE⊥平面ABCD,所以EO⊥面ABCD。
连结OD,则∠ODE为直线DE与平面ABCD所成的角。 (8分)
设圆柱的底半径为r,则其底面积为![]() ,
,
△ABE的面积为![]() 。
。
由已知,![]() ,则OE=r,所以点O为圆柱底面圆的圆心。 (10分)
,则OE=r,所以点O为圆柱底面圆的圆心。 (10分)
在Rt△OAD中,![]() ,在Rt△DOE中
,在Rt△DOE中 ![]() 。
。
故直线DE与平面ABCD所成角的正切值为![]() 。 (12分)
。 (12分)

练习册系列答案
相关题目
 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 
 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.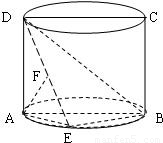
 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007