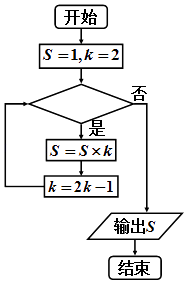
题目内容
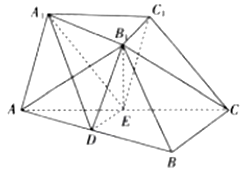
【题目】如图,在三棱台 ![]() 中,
中, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() 的中点,
的中点, ![]() ,
, ![]() 平面
平面 ![]() ,且
,且 ![]() .
.
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,
, ![]() 为等边三角形,求四棱锥
为等边三角形,求四棱锥 ![]() 的体积.
的体积.
【答案】
(1)解:设 ![]() 与
与 ![]() 相交于
相交于 ![]() ,连接
,连接 ![]() ,
,
由题意可知, ![]() ,
, ![]() ,
,
所以四边形 ![]() 是平行四边形,
是平行四边形,
从而 ![]() 是
是 ![]() 的中点.
的中点.
又 ![]() 是
是 ![]() 的中点,
的中点,
所以 ![]() .
.
又 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]()
(2)解:易证 ![]() ,
, ![]() 是三棱柱,
是三棱柱,
又因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 是此三棱柱的高,
是此三棱柱的高,
同理 ![]() 也是三棱锥
也是三棱锥 ![]() 的高.
的高.
因为 ![]() ,
, ![]() 为等边三角形,
为等边三角形,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
又 ![]() ,
,
所以 ![]() .
.
【解析】本题考查线面平行的证明,考查四棱锥的体积的求法.直线与平面平行的判定定理的实质是:对于平面外的一条直线,只需在平面内找到一条直线和这条直线平行,就可判定这条直线必和这个平面平行.即由线线平行得到线面平行.柱体、锥体、台体的体积公式:
V柱=sh,V锥=![]() Sh.
Sh.
【考点精析】本题主要考查了棱锥的结构特征和棱台的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方;①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点才能正确解答此题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目