题目内容
设函数f(x)= (x>0),观察f1(x)=f(x)=
(x>0),观察f1(x)=f(x)= ,
,
f2(x)=f[f1(x)]=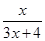 ,
,
f3(x)=f[f2(x)]= ,
,
f4(x)=f[f3(x)]= ,…
,…
根据以上事实,由归纳推理可得:当n∈N+且n≥2时,fn(x)=f[fn-1(x)]=________.
 (x>0),观察f1(x)=f(x)=
(x>0),观察f1(x)=f(x)= ,
,f2(x)=f[f1(x)]=
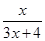 ,
,f3(x)=f[f2(x)]=
 ,
,f4(x)=f[f3(x)]=
 ,…
,…根据以上事实,由归纳推理可得:当n∈N+且n≥2时,fn(x)=f[fn-1(x)]=________.

先求分母中x项系数组成数列的通项公式,由1,3,7,15…,可推知该数列的通项公式为an=2n-1,又函数结果分母中常数项依次为2,4,8,16,…,故其通项公式为bn=2n.∴fn(x)= .
.
 .
.
练习册系列答案
相关题目
 ”可选择的方法有以下几种,其中最合理的是 。(填序号)
”可选择的方法有以下几种,其中最合理的是 。(填序号)
 =2
=2 ,
, =3
=3 ,
,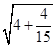 =4
=4 ,…,若
,…,若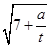 =7
=7 ,(a,t均为正实数),则类比以上等式,可推测a、t的值,a+t= .
,(a,t均为正实数),则类比以上等式,可推测a、t的值,a+t= . 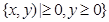 内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么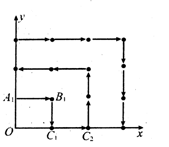
 ,1+
,1+ >1,1+
>1,1+
 ,1+
,1+ >2,1+
>2,1+ >
> ,…,由此猜测第n个不等式为________(n∈N+).
,…,由此猜测第n个不等式为________(n∈N+).