题目内容
13.已知P是直线l:x+my+4=0上一动点,PA、PB是圆C:x2+y2-2x=0的两条切线,切点分别为A、B,若四边形PACB的最小面积为2,则实数m=( )| A. | 2或-2 | B. | 2 | C. | -2 | D. | 无数个取值 |
分析 先求圆的半径,四边形PACB的最小面积是2,转化为三角形PBC的面积是1,求出切线长,再求PC的距离也就是圆心到直线的距离,可解m的值.
解答 解:圆C:x2+y2-2x=0的圆心(1,0),半径是r=1,
由圆的性质知:S四边形PACB=2S△PBC,四边形PACB的最小面积是2.
∴S△PBC的最小值S=1=$\frac{1}{2}$rd(d是切线长)
∴d最小值=2
圆心到直线的距离就是PC的最小值,$\sqrt{1+4}=\frac{5}{\sqrt{1+{m}^{2}}}$
∴m=±2
故选:A.
点评 本题考查直线和圆的方程的应用,点到直线的距离公式等知识,是中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
1.设集合M={x|x<3},N={x|x>-1},全集U=R,则∁U(M∩N)=( )
| A. | {x|x≤-1} | B. | {x|x≥3} | C. | {x|0<x<3} | D. | {x|x≤-1或x≥3} |
8.广丰一中现有职工180人,其中高级职称42人,中级职称78人,一般职员60人,现抽取30人进行分层抽样,则各职称人数分别为( )
| A. | 5,15,10 | B. | 3,18,9 | C. | 7,13,10 | D. | 5,16,9 |
18.一个样本的数据在60左右波动,各个数据都减去60后得到一组新数据,算得其平均数是6,则这个样本的平均数是( )
| A. | 6.6 | B. | 6 | C. | 66 | D. | 60 |
3.将${({1-\frac{1}{x^2}})^n}(n∈{N_+})$的展开式中x-4的系数记为an,则$\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{{{a_{2016}}}}$等于( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | 2015 | D. | 2016 |
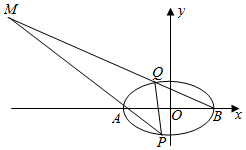 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{3}$,且椭圆的四个顶点相连得到的凸四边形的面积为12$\sqrt{2}$.