题目内容
如图,已知椭圆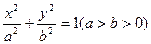 的长轴
的长轴 ,离心率
,离心率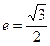 ,
,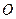 为坐标原点,过
为坐标原点,过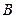 的直线
的直线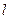 与
与 轴垂直,
轴垂直,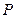 是椭圆上异于
是椭圆上异于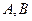 的任意一点,
的任意一点,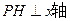 ,
,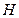 为垂足,延长
为垂足,延长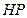 至
至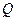 ,使得
,使得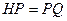 ,连接
,连接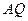 并延长交直线
并延长交直线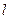 于
于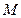 ,
,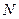 为
为 的中点
的中点
(1)求椭圆方程并证明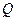 点在以
点在以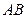 为直径的圆
为直径的圆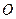 上
上
(2)试判断直线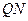 与圆
与圆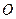 的位置关系
的位置关系
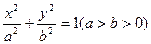 的长轴
的长轴 ,离心率
,离心率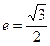 ,
,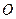 为坐标原点,过
为坐标原点,过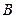 的直线
的直线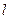 与
与 轴垂直,
轴垂直,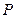 是椭圆上异于
是椭圆上异于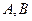 的任意一点,
的任意一点,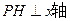 ,
,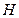 为垂足,延长
为垂足,延长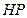 至
至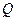 ,使得
,使得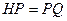 ,连接
,连接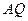 并延长交直线
并延长交直线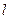 于
于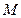 ,
,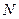 为
为 的中点
的中点(1)求椭圆方程并证明
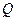 点在以
点在以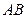 为直径的圆
为直径的圆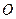 上
上(2)试判断直线
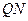 与圆
与圆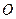 的位置关系
的位置关系 |
(1)见解析(2)见解析
(1)由已知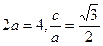 ,所以
,所以 ,所以椭圆的方程为
,所以椭圆的方程为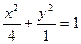 ,
,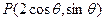
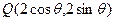 ,
,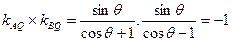
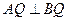 得证
得证
(2)直线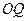 的斜率为
的斜率为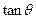 ,倾斜角∠
,倾斜角∠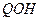
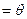 ,
,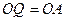 得∠
得∠ ∠
∠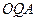
 ,即直线
,即直线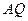 的倾斜角为
的倾斜角为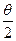 ,所以直线
,所以直线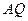 的方程为
的方程为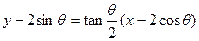 ,
,
令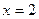 得
得 ,所以
,所以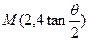 ,
,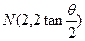 ,所以直线
,所以直线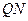 的斜率为
的斜率为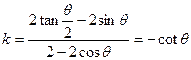 ,
,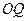 的斜率为
的斜率为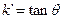 ,所以
,所以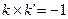 ,即
,即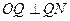 ,
,
且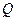 点在以
点在以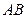 为直径的圆
为直径的圆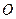 上,所以
上,所以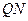 与圆
与圆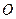 相切于
相切于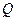 点
点
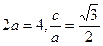 ,所以
,所以 ,所以椭圆的方程为
,所以椭圆的方程为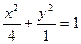 ,
,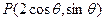
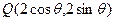 ,
,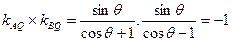
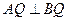 得证
得证(2)直线
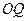 的斜率为
的斜率为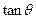 ,倾斜角∠
,倾斜角∠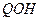
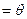 ,
,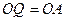 得∠
得∠ ∠
∠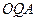
 ,即直线
,即直线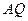 的倾斜角为
的倾斜角为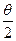 ,所以直线
,所以直线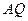 的方程为
的方程为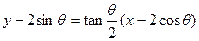 ,
,令
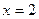 得
得 ,所以
,所以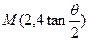 ,
,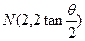 ,所以直线
,所以直线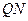 的斜率为
的斜率为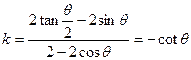 ,
,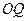 的斜率为
的斜率为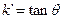 ,所以
,所以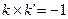 ,即
,即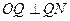 ,
,且
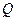 点在以
点在以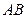 为直径的圆
为直径的圆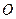 上,所以
上,所以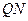 与圆
与圆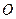 相切于
相切于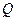 点
点
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

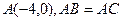 ,且
,且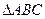 的内切圆方程为
的内切圆方程为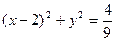 .
.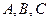 三点的椭圆标准方程;
三点的椭圆标准方程; 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点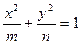 ,常数
,常数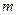 、
、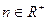 ,且
,且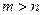 .
. 当
当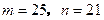 时,过椭圆左焦点
时,过椭圆左焦点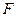 的直线交椭圆于点
的直线交椭圆于点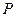 ,与
,与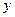 轴交于点
轴交于点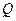 ,若
,若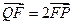 ,求直线
,求直线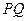 的斜率;
的斜率;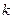 和
和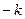 (
(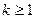 )的两条直
)的两条直 线与椭圆
线与椭圆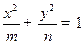 的交点为
的交点为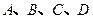 (按逆时针顺序排列,且点
(按逆时针顺序排列,且点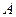 位于第一象限内),试用
位于第一象限内),试用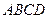 的面积
的面积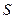 ;
;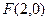 ,且两条准线间的距离为
,且两条准线间的距离为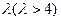 。
。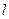 ,使点F关于直线
,使点F关于直线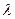 的取值范围。
的取值范围。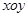 中,已知△
中,已知△ 顶点
顶点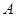 (-4,0)和
(-4,0)和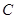 (4,0),顶点
(4,0),顶点 在椭圆
在椭圆 上,则
上,则 = ( )
= ( )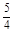
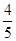
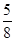
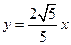 和
和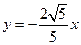 上的两个动点,并且
上的两个动点,并且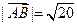 ,动点P满足
,动点P满足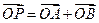 .记动点P的轨迹为C.
.记动点P的轨迹为C.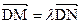 ,求实数
,求实数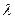 的取值范围.
的取值范围.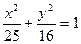 上的一点,△
上的一点,△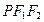 的内切圆半径是
的内切圆半径是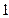 ,求
,求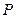 的坐标
的坐标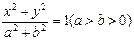 的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,
的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,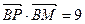 ,若点P的坐标为(0,t),则t的取值范围是 ( )
,若点P的坐标为(0,t),则t的取值范围是 ( )
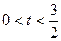
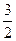
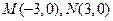 ,若直线上存在点P,使得
,若直线上存在点P,使得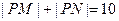 ,则称该直线为“A型直线”。给出下列直线:①
,则称该直线为“A型直线”。给出下列直线:① ;②
;②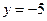 ;③
;③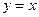 ;④
;④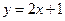 ,其中是“A型直线”的是
,其中是“A型直线”的是