题目内容
17.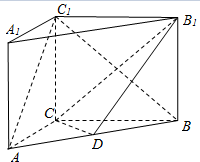 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.
(Ⅲ)设AB=2AA1,AC=BC,在线段A1B1上是否存在点M,使得BM⊥CB1?若存在,确定点M的位置;若不存在,说明理由.
分析 (I)先证明CC1⊥AC,又AC⊥BC,BC∩CC1=C,可证AC⊥平面BCC1B1,从而可证AC⊥BC1.
(Ⅱ)设CB1与C1B的交点为E,连结DE,可证DE∥AC1.即可判定AC1∥平面CDB1.
(Ⅲ)可证AA1⊥CD,CD⊥AB,从而证明CD⊥平面AA1B1B,取线段A1B1的中点M,连接BM.可证CD⊥BM,BM⊥B1D,即可证明BM⊥平面B1CD,从而得证BM⊥CB1.
解答 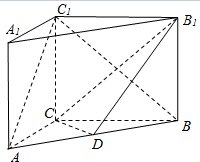 (本小题满分14分)
(本小题满分14分)
证明:(I)在三棱柱ABC-A1B1C1中,因为CC1⊥底面ABC,AC?底面ABC,
所以CC1⊥AC.
又AC⊥BC,BC∩CC1=C,
所以AC⊥平面BCC1B1.
而BC1?平面BCC1B1,
则AC⊥BC1.…(4分)
(Ⅱ)设CB1与C1B的交点为E,连结DE,
因为D是AB的中点,E是BC1的中点,
所以DE∥AC1.
因为DE?平面CDB1,AC1?平面CDB1,
所以AC1∥平面CDB1.…(9分)
(Ⅲ)在线段A1B1上存在点M,使得BM⊥CB1,且M为线段A1B1的中点.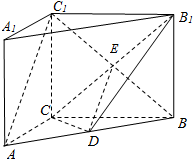
证明如下:因为AA1⊥底面ABC,CD?底面ABC,
所以AA1⊥CD.
由已知AC=BC,D为线段AB的中点,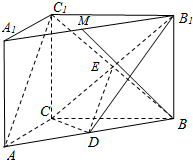
所以CD⊥AB.
又AA1∩AB=A,
所以CD⊥平面AA1B1B.
取线段A1B1的中点M,连接BM.
因为BM?平面AA1B1B,所以CD⊥BM.
由已知AB=2AA1,由平面几何知识可得BM⊥B1D.
又CD∩B1D=D,所以BM⊥平面B1CD.
又B1C?平面B1CD,
所以BM⊥CB1.…(14分)
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定和性质,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.已知数列{an}中,a1=1,且满足an+1=an+2n,n∈N+,则a10=( )
| A. | 19 | B. | 91 | C. | 101 | D. | 121 |
9.设f(x)=cosx-sinx,把f(x)的图象按向量$\overrightarrow{a}$=(m,0)(m>0)平移后,图象恰好为函数y=-f′(x)的图象,则m的值可以为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | π | D. | $\frac{π}{2}$ |
7.在复平面内复数$z=\frac{ai+1}{1-i}$对应的点在第一象限,则实数a的取值可以为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.