题目内容
已知P为双曲线 左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF2F1=sin∠PF1F2=
左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF2F1=sin∠PF1F2= ,则此双曲线离心率是 .
,则此双曲线离心率是 .
【答案】分析:写判断PF2⊥PF1,由直角三角形中的边角关系及同角三角函数的基本关系求出PF2 和PF1 的值,再利用双曲线的定义求得 的值.
的值.
解答:解:△PF2F1中,∵cos∠PF2F1=sin∠PF1F2= ,∴∠PF2F1 与∠PF1F2互为余角,
,∴∠PF2F1 与∠PF1F2互为余角,
PF2⊥PF1,∴ =sin∠PF1F2=
=sin∠PF1F2= ,PF2=
,PF2= ,∴cos∠PF1F2 =
,∴cos∠PF1F2 = =
= ,
,
∴PF1= ,再由双曲线的定义得 PF1-PF2=2a,即
,再由双曲线的定义得 PF1-PF2=2a,即  =2a,
=2a,
 =
= ,
,
故答案为 .
.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,其中,判断PF2⊥PF1是解题的关键.
 的值.
的值.解答:解:△PF2F1中,∵cos∠PF2F1=sin∠PF1F2=
 ,∴∠PF2F1 与∠PF1F2互为余角,
,∴∠PF2F1 与∠PF1F2互为余角,PF2⊥PF1,∴
 =sin∠PF1F2=
=sin∠PF1F2= ,PF2=
,PF2= ,∴cos∠PF1F2 =
,∴cos∠PF1F2 = =
= ,
,∴PF1=
 ,再由双曲线的定义得 PF1-PF2=2a,即
,再由双曲线的定义得 PF1-PF2=2a,即  =2a,
=2a, =
= ,
,故答案为
 .
.点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,其中,判断PF2⊥PF1是解题的关键.

练习册系列答案
相关题目
 左支上一点,
左支上一点, 为双曲线的左右焦点,且
为双曲线的左右焦点,且
 则此双曲线离心率是
.
则此双曲线离心率是
.  左支上一点,
左支上一点, 分别为双曲线的左、右焦点,若
分别为双曲线的左、右焦点,若 ,则此双曲线离心率是
,则此双曲线离心率是 B.5
C.2
B.5
C.2 左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF1F2=sin∠PF2F1=
左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF1F2=sin∠PF2F1=
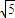

 左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF2F1=sin∠PF1F2=
左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF2F1=sin∠PF1F2=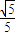 ,则此双曲线离心率是 .
,则此双曲线离心率是 . 左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF1F2=sin∠PF2F1=
左支上一点,F1,F2为双曲线的左右焦点,且cos∠PF1F2=sin∠PF2F1=

