题目内容
已知P为双曲线
左支上一点，F1，F2为双曲线的左右焦点，且cos∠PF1F2=sin∠PF2F1=
则此双曲线离心率是（ ）
A．
B．5
C．2
D．3
【答案】分析：先根据cos∠PF1F2=sin∠PF2F1推断△PF1F2为直角三角形，设|PF1|=x，||PF2|=y，根据勾股定理可知x2+y2=4c2，同时又根据正弦定理可得
得出x与y的关系，联立方程求得x和y，进而根据双曲线定义y-x=2a，从而找到a和c的关系，求得离心率e．
解答：解：cos∠PF1F2=sin∠PF2F1
∴90°-∠PF1F2=∠PF2F1，即90°=∠PF1F2+∠PF2F1
设|PF1|=x，||PF2|=y
则有x2+y2=4c2，①
根据正弦定理
=
即
∴2x=y②
①②联立方程求得x=
，y=
c
∴根据双曲线定义可知y-x=
c=2a
∴e=
=
故选A
点评：本题主要考查了双曲线的简单性质．考查了用定义法来解决圆锥曲线的问题．
得出x与y的关系，联立方程求得x和y，进而根据双曲线定义y-x=2a，从而找到a和c的关系，求得离心率e．解答：解：cos∠PF1F2=sin∠PF2F1
∴90°-∠PF1F2=∠PF2F1，即90°=∠PF1F2+∠PF2F1
设|PF1|=x，||PF2|=y
则有x2+y2=4c2，①
根据正弦定理
=即
∴2x=y②
①②联立方程求得x=
，y=c∴根据双曲线定义可知y-x=
c=2a∴e=
=故选A
点评：本题主要考查了双曲线的简单性质．考查了用定义法来解决圆锥曲线的问题．
练习册系列答案
相关题目
左支上一点，
为双曲线的左右焦点，且
则此双曲线离心率是
． 
左支上一点,
分别为双曲线的左、右焦点,若
,则此双曲线离心率是
B.5
C.2
左支上一点，F1，F2为双曲线的左右焦点，且cos∠PF1F2=sin∠PF2F1=
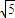
左支上一点，F1，F2为双曲线的左右焦点，且cos∠PF2F1=sin∠PF1F2=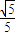
，则此双曲线离心率是 ．