题目内容
11.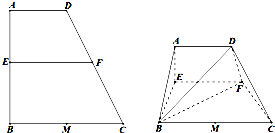 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.(1)当x=2时,求证:BD⊥EM;
(2)当x变化时,求四棱锥D-BCEF的体积f(x)的函数式.
分析 (1)作DH⊥EF于H,连结BH,MH,EM,证明DH⊥平面EBCF.然后推出EM⊥平面BDH.即可证明EM⊥BD.(2)设DH=AE=x为四棱锥D-BCFE的高,求出底面面积然后求解体积的函数解析式.
解答 解析:(1)证明:如图,作DH⊥EF于H,连结BH,MH,EM,∵平面AEFD⊥平面EBCF,∴DH⊥平面EBCF.
又EM?平面EBCF,∴EM⊥DH.∵$EH=AD=\frac{1}{2}BC$,EF∥BC,∠EBC=90°,
∴四边形BMHE为正方形,∴EM⊥BH.∴EM⊥平面BDH.
又BD?平面BDH,
∴EM⊥BD.…(6分)
(2)由(1)知,DH=AE=x为四棱锥D-BCFE的高,∵AE=x,∴BE=4-x,$EF=2+\frac{1}{2}x$,
∴$\begin{array}{c}{S}_{BCFE}=\frac{1}{2}(EF+BC)•BE=\frac{1}{2}(2+\frac{1}{2}x+4)•(4-x)\end{array}\right.$=$\begin{array}{c}\\-\frac{1}{4}{x}^{2}-2x+12.\end{array}\right.$,
∴$f(x)=\frac{1}{3}{S_{BCFE}}•x=-\frac{1}{12}{x^3}-\frac{2}{3}{x^2}+4x$.…(12分)
点评 本题考查直线与平面垂直的判断与性质定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知抛物线y2=8x的焦点与双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1的一个焦点重合,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{4\sqrt{15}}}{15}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{2}$ |
6.已知I为△ABC所在平面上的一点,且AB=c,AC=b,BC=a.若a$\overrightarrow{IA}$+b$\overrightarrow{IB}$+c$\overrightarrow{IC}$=$\overrightarrow{0}$,则I一定是△ABC的( )
| A. | 垂心 | B. | 内心 | C. | 外心 | D. | 重心 |
20.设a,b∈R,则a2(a-b)>0是a>b的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
1.在平面直角坐标系中,把横、纵坐标均为有理数的点称为有理点.若a为无理数,则在过点P(a,-$\frac{1}{2}$)的所有直线中( )
| A. | 有无穷多条直线,每条直线上至少存在两个有理点 | |
| B. | 恰有n(n≥2)条直线,每条直线上至少存在两个有理点 | |
| C. | 有且仅有一条直线至少过两个有理点 | |
| D. | 每条直线至多过一个有理点 |
 如图,CE为圆O的直径,PE为圆O的切线,E为切点,PBA为圆O的割线,交CE于D点,CD=2,AD=3,BD=4,则圆O的半径为r=4;PB=20.
如图,CE为圆O的直径,PE为圆O的切线,E为切点,PBA为圆O的割线,交CE于D点,CD=2,AD=3,BD=4,则圆O的半径为r=4;PB=20.