题目内容
已知函数f(x)= x3-a2x+2a,(a>0)
x3-a2x+2a,(a>0)(1)求函数y=f(x)的单调区间;
(2)若在区间[0,2]上恒有f(x)≥-
 ,求a的取值范围.
,求a的取值范围.
【答案】分析:(1)先对函数f(x)进行求导,令导函数大于0可求函数的增区间,令导函数小于0可求函数的减区间.
(2)在区间[0,2]上恒有f(x)≥- ,等价于x∈[0,2]时f(x)min≥-
,等价于x∈[0,2]时f(x)min≥- ,借助(1)问函数的单调性可求其最小值.
,借助(1)问函数的单调性可求其最小值.
解答:解:(1)f'(x)=x2-a2=(x-a)(x+a)(a>0)
f'(x)>0⇒x>a或x<-a,f'(x)<0⇒-a<x<a…(4分)
∴f(x)在(-∞,-a)和(a,+∞)上都单调递增,在[-a,a]上单调递减;…(6分)
(2)x=-a为函数y=f(x)的极大值点,x=a为函数y=f(x)的极小值点,…(8分)
①当0<a<2时,函数y=f(x)在[0,2]上的最小值为f(a)=- a3+2a,
a3+2a,
∴- a3+2a
a3+2a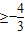 ,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2
,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2
∴0<a<2…(11分)
②当a≥2时,函数y=f(x)在[0,2]上的最小值为f(2)=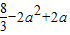 ,
,
∴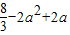
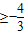 ,∴-1≤a≤2
,∴-1≤a≤2
又a≥2,∴a=2,…(14分)
综上,0<a≤2.…(15分).
点评:本题考查的知识点是利用导数求闭区间上函数的最值,利用导数研究函数的单调性,熟练掌握导函数法求函数单调区间和最值的方法和步骤是解答的关键.
(2)在区间[0,2]上恒有f(x)≥-
 ,等价于x∈[0,2]时f(x)min≥-
,等价于x∈[0,2]时f(x)min≥- ,借助(1)问函数的单调性可求其最小值.
,借助(1)问函数的单调性可求其最小值.解答:解:(1)f'(x)=x2-a2=(x-a)(x+a)(a>0)
f'(x)>0⇒x>a或x<-a,f'(x)<0⇒-a<x<a…(4分)
∴f(x)在(-∞,-a)和(a,+∞)上都单调递增,在[-a,a]上单调递减;…(6分)
(2)x=-a为函数y=f(x)的极大值点,x=a为函数y=f(x)的极小值点,…(8分)
①当0<a<2时,函数y=f(x)在[0,2]上的最小值为f(a)=-
 a3+2a,
a3+2a,∴-
 a3+2a
a3+2a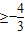 ,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2
,即(a+1)2(a-2)≤0,∴a≤2,又0<a<2∴0<a<2…(11分)
②当a≥2时,函数y=f(x)在[0,2]上的最小值为f(2)=
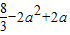 ,
,∴
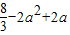
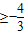 ,∴-1≤a≤2
,∴-1≤a≤2又a≥2,∴a=2,…(14分)
综上,0<a≤2.…(15分).
点评:本题考查的知识点是利用导数求闭区间上函数的最值,利用导数研究函数的单调性,熟练掌握导函数法求函数单调区间和最值的方法和步骤是解答的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|