题目内容
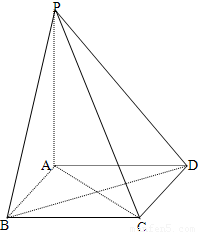
P为四边形ABCD所在平面上一点，
+
+
+
=
+
，则P为（ ）
| PA |
| PB |
| PC |
| PD |
| AB |
| CD |
| A、四边形ABCD对角线交点 |
| B、AC中点 |
| C、BD中点 |
| D、CD边上一点 |
分析：利用向量的三角形法则可得：
=
+
，
=
+
．由于
+
+
+
=
+
，
可得
+
=
+
，即
+
=
．即可得出．
| AB |
| AP |
| PB |
| CD |
| CP |
| PD |
| PA |
| PB |
| PC |
| PD |
| AB |
| CD |
可得
| PA |
| PC |
| AP |
| CP |
| PA |
| PC |
| 0 |
解答：解：∵
=
+
，
=
+
．
又
+
+
+
=
+
，
∴
+
=
+
，
∴
+
=
．
∴点P为线段AC的中点．
故选：B．
| AB |
| AP |
| PB |
| CD |
| CP |
| PD |
又
| PA |
| PB |
| PC |
| PD |
| AB |
| CD |
∴
| PA |
| PC |
| AP |
| CP |
∴
| PA |
| PC |
| 0 |
∴点P为线段AC的中点．
故选：B．
点评：本题考查了向量的三角形法则和中点公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
ABCD为平行四边形，P为平面ABCD外一点，PA⊥面ABCD，且PA=AD=2，AB=1，AC=
a.
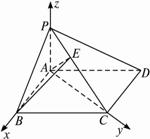
的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD．若G为AD的中点，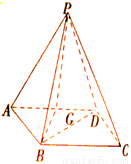
．
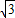