题目内容
ABCD是平行四边形,P为平面ABCD外一点,PA⊥面ABCD,且PA=AD=2a,AB=a,AC=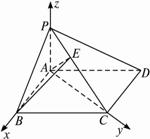
(1)求证:平面ABCD⊥平面PAC;
(2)求异面直线PC与BD所成角的余弦值;
(3)设二面角A-PC-B的大小为θ,求tanθ的值.
(1)证明:∵AB=a,AD=2a,AC=![]() a,∴∠BAC=∠ACD=90°.?
a,∴∠BAC=∠ACD=90°.?
 ?
?
∵PA⊥面ABCD,PA![]() 面PAC,∴面PAC⊥面ABCD.?
面PAC,∴面PAC⊥面ABCD.?
(2)解析:建立如图所示坐标系.
B(a,0,0),D(-a,![]() a,0),C(0,
a,0),C(0,![]() a,0),P(0,0,2a)?,
a,0),P(0,0,2a)?,![]() =(-2a,
=(-2a,![]() a,0),
a,0),![]() =(0,
=(0,![]() a,-2a),?
a,-2a),?
∴cosα=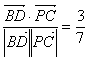 .?
.?
(3)解析:∵∠BAC=90°,?
∴BA⊥AC,PA⊥面ABCD.?
∴PA⊥AB.?
∴AB⊥面PAC.?
作AE⊥PC,连结BE,?
∴∠AEB即为所求角θ.?
∵AP=2a,AC=![]() a,PC=
a,PC=![]() a,?
a,?
∴AE=![]() .?
.?
∴tanθ=![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
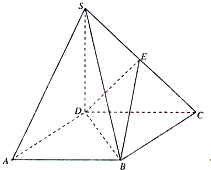 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,
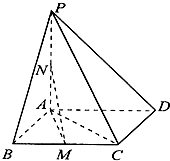 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC= 如图,已知四棱锥V-ABCD,底面ABCD是平行四边形,点V在平面ABCD上的射影E在AD边上,且
如图,已知四棱锥V-ABCD,底面ABCD是平行四边形,点V在平面ABCD上的射影E在AD边上,且