题目内容
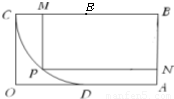
如图，矩形OABC中，AB=1，OA=2，以BC中点E为圆心、以1为半径在矩形内部作四分之一圆弧CD（其中D为OA中点），点P是弧CD上一动点，PM⊥BC，垂足为M，PN⊥AB，垂足为N，则四边形PMBN的周长的最大值为________．
分析：设∠MBP=α，利用α的三角函数表示出四边形PMBN的周长，再利用辅助角公式化简，即可求得四边形PMBN的周长的最大值．
解答：设∠MBP=α，则
∴BM=cosα，PM=sinα
∴四边形PMBN的周长为2+2（cosα+sinα）=2+2
sin（α+
） ∵
∴
∴sin（α+
）max=1∴2+2
sin（α+）的最大值为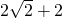故答案
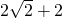
点评：本题考查圆的方程综合应用，解题的关键是引进角参数，利用三角函数进行求解．
练习册系列答案
阅读快车系列答案
相关题目
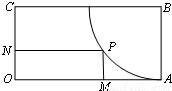
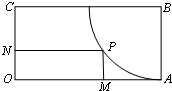（2012•闵行区一模）如图，矩形OABC中，AB=1，OA=2，以B为圆心、BA为半径在矩形内部作弧，点P是弧上一动点，PM⊥OA，垂足为M，PN⊥OC，垂足为N，则四边形OMPN的周长的最小值为
（2012•闵行区一模）如图，矩形OABC中，AB=1，OA=2，以BC中点E为圆心、以1为半径在矩形内部作四分之一圆弧CD（其中D为OA中点），点P是弧CD上一动点，PM⊥BC，垂足为M，PN⊥AB，垂足为N，则四边形PMBN的周长的最大值为
，垂足为M，
，垂足为N，则四边形OMPN的周长的最小值为
．
