题目内容
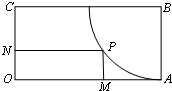 (2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为
(2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为6-2
| 2 |
6-2
.| 2 |
分析:连接BP,设∠CBP=α,其中0≤α<
,则PM=1-sinα,PN=2-cosα,周长C=6-2(sinα+cosα),再利用三角函数恒等变换,能求出四边形OMPN的周长的最小值.
| π |
| 2 |
解答:解:连接BP,设∠CBP=α,其中0≤α<
,
则PM=1-sinα,PN=2-cosα
周长C=6-2(sinα+cosα),
∵(sinα+cosα)2=1+2sinαcosα=1+sin2α,
∴要让周长最小,即让(sinα+cosα)最大,即sin2α最大,
∵sin2α在α=
时取到最大值sin2α=1,
∴当α=
时,周长有最小值6-2
.
故答案为:6-2
.
| π |
| 2 |
则PM=1-sinα,PN=2-cosα
周长C=6-2(sinα+cosα),
∵(sinα+cosα)2=1+2sinαcosα=1+sin2α,
∴要让周长最小,即让(sinα+cosα)最大,即sin2α最大,
∵sin2α在α=
| π |
| 4 |
∴当α=
| π |
| 4 |
| 2 |
故答案为:6-2
| 2 |
点评:本题考查四边形周长的最小值的求法,具体涉及到圆的简单性质、三角函数等基本知识,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 (2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是
(2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是 (2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足
(2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足