题目内容
在R上定义运算：对x,y
R,有x
y=2x+y，如果a3b=1(ab>0)，则
的最小值是（ ）
A． | B． | C． | D． |
B
解析试题分析：依题意问题转化为已知
，求
的最小值。
因为
且
，
当且仅当
时“=”成立。故B正确。
考点：1新概念；2基本不等式。
练习册系列答案
相关题目
已知命题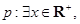
使得
；命题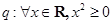
.则下列命题为真命题的是（ ）
A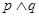． | B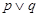． | C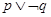． | D． |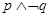
若正数
满足：
，则
的最小值为（ ）
A． | B． | C． | D． |
若a、b∈R，且ab＞0，则下列不等式中，恒成立的是( )．
| A．a2＋b2＞2ab | B．a＋b≥2 |
C． | D． |
设
为坐标原点，第一象限内的点
的坐标满足约束条件
，
，若
的最大值为40，则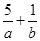
的最小值为（ ）
A． | B． | C．1 | D．4 |
若正数x,y满足x+3y=5xy,则3x+4y的最小值是( )
A． | B． | C．5 | D．6 |
若直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则
+
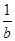的最小值为( )
A． | B． |
C． + | D．+2 |
已知a>0,b>0,且2是2a与b的等差中项,则
的最小值为( )
A． | B． | C．2 | D．4 |
