题目内容
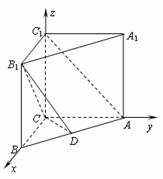
直三棱柱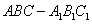 中,
中,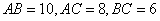 ,
,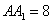 ,点D在线段AB上.
,点D在线段AB上.
(Ⅰ)若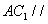 平面
平面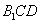 ,确定D点的位置并证明;
,确定D点的位置并证明;
(Ⅱ)当 时,求二面角
时,求二面角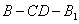 的余弦值.
的余弦值.
(Ⅰ)证明:当D是AB中点时,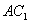 ∥平面
∥平面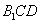 .
.
连接BC1,交B1C于E,连接DE.
因为三棱柱ABC-A1B1C1是直三棱柱,
所以侧面BB1C1C为矩形,DE为△ABC1的中位线,
所以 DE// AC1.
因为 DE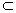 平面B1CD, AC1
平面B1CD, AC1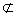 平面B1CD,
平面B1CD,
所以 AC1∥平面B1CD.
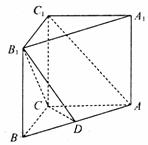
(Ⅱ)由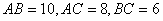 ,得AC⊥BC,以C为原点建立如图所示的空间直角坐标系C-xyz.则B(6, 0, 0),A (0, 8, 0),A1(0, 8,8),B1(6, 0, 8).设D(a, b, 0)(
,得AC⊥BC,以C为原点建立如图所示的空间直角坐标系C-xyz.则B(6, 0, 0),A (0, 8, 0),A1(0, 8,8),B1(6, 0, 8).设D(a, b, 0)(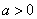 ,
, ),
),
因为 点D在线段AB上,且 , 即
, 即 .
.
所以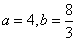 .
.
所以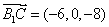 ,
,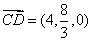 .
.
平面BCD的法向量为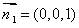 .
.
设平面B1CD的法向量为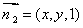 ,
,
由 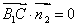 ,
,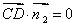 , 得
, 得 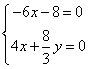 ,
,
所以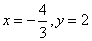 ,
,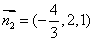 .
.
设二面角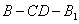 的大小为
的大小为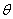 ,
,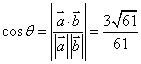 .
.
所以二面角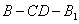 的余弦值为
的余弦值为 .
.

练习册系列答案
相关题目
某餐厅的原料费支出 与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为
与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为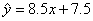 ,则表中的m的值为
,则表中的m的值为
|
| 2 | 4 | 5 | 6 | 8 |
|
| 25 | 35 |
| 55 | 75 |
A.50 B.55 C.60 D.65
 ,则
,则 = 0 ;不等式
= 0 ;不等式 的解集为______.
的解集为______. 、
、 两个小孩和甲、乙、丙三个大人排队,
两个小孩和甲、乙、丙三个大人排队,

 的扇形,则该几何体的体积为__________.
的扇形,则该几何体的体积为__________.
 ,其中i为虚数为单位,则Z=
,其中i为虚数为单位,则Z= 相切,则反射光线所在直线的斜率为()
相切,则反射光线所在直线的斜率为() 或
或 (B
(B 或
或
 或
或 (D)
(D) 或
或
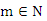 , 如题“m>0,则方程
, 如题“m>0,则方程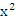
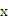
 有实根的逆否命题是
有实根的逆否命题是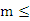
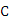 若方程
若方程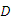 若方程
若方程