题目内容
设函数f(x)=x3+ax2+bx+c在x=1处取得极值-2,试用c表示a和b,并求f(x)的单调区间。
解:依题意有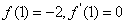 ,而
,而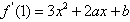 ,
,
故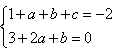 ,解得
,解得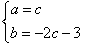 ,
,
从而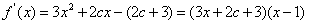 ,
,
令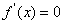 ,得x=1或
,得x=1或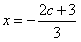 ,
,
由于f(x)在x=1处取得极值,故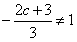 ,即c≠-3,
,即c≠-3,
(1)若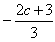 <1,即c>-3,则当
<1,即c>-3,则当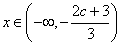 时,
时,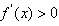 ;
;
当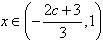 时,
时,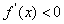 ;当
;当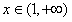 时,
时,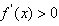 ;
;
从而f(x)的单调增区间为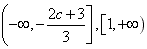 ;单调减区间为
;单调减区间为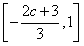 ;
;
(2)若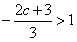 ,即c<-3,同上可得,f(x)的单调增区间为
,即c<-3,同上可得,f(x)的单调增区间为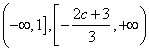 ;
;
单调减区间为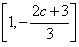 。
。
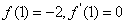 ,而
,而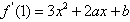 ,
,故
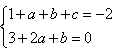 ,解得
,解得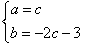 ,
,从而
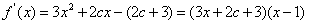 ,
,令
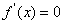 ,得x=1或
,得x=1或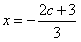 ,
,由于f(x)在x=1处取得极值,故
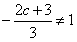 ,即c≠-3,
,即c≠-3,(1)若
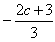 <1,即c>-3,则当
<1,即c>-3,则当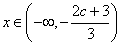 时,
时,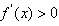 ;
;当
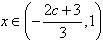 时,
时,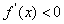 ;当
;当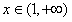 时,
时,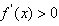 ;
;从而f(x)的单调增区间为
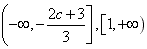 ;单调减区间为
;单调减区间为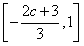 ;
;(2)若
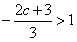 ,即c<-3,同上可得,f(x)的单调增区间为
,即c<-3,同上可得,f(x)的单调增区间为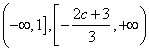 ;
;单调减区间为
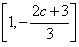 。
。 
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
设函数f(x)=x3-(
)x-2,则其零点所在区间为( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |