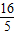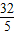题目内容
过椭圆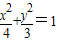
的右焦点F作倾斜角为
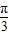的弦AB，则|AB|=（ ）A．
B．
C．
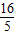
D．
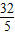
【答案】分析：由题意知AB所在的直线方程为y=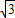
（x-1），把y=
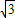（x-1）代入椭圆
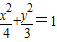后，利用弦长公式可以求出|AB|的值．
解答：解：由题意知F（1.0），k=tan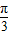
=
，
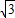∴过椭圆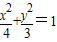
的右焦点F作倾斜角为
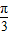的直线方程为y=
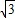（x-1），
把y=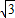
（x-1）代入椭圆方程，并整理，得
5x2-8x=0，
设直线与椭圆交于A（x1，y1），B（x2，y2），
x1=0，x2=
，
∴A（0，-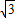
），B（
，
）
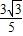∴|AB|=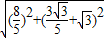
=
．
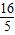故选C．
点评：本题考查椭圆的性质和应用，解题时要认真审题，注意弦长公式的应用．
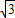（x-1），把y=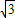（x-1）代入椭圆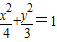后，利用弦长公式可以求出|AB|的值．解答：解：由题意知F（1.0），k=tan
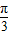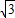=，∴过椭圆
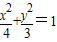的右焦点F作倾斜角为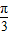的直线方程为y=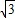（x-1），把y=
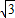（x-1）代入椭圆方程，并整理，得5x2-8x=0，
设直线与椭圆交于A（x1，y1），B（x2，y2），
x1=0，x2=
，∴A（0，-
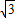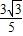），B（，）∴|AB|=
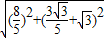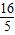=．故选C．
点评：本题考查椭圆的性质和应用，解题时要认真审题，注意弦长公式的应用．
练习册系列答案
快乐5加2金卷系列答案
相关题目
（2006•海淀区一模）如图，椭圆
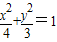的右焦点F作倾斜角为
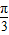的弦AB，则|AB|=（ ）
的右焦点F作倾斜角为
的直线
交椭圆于A、B两点，P为右准线上一点，使
的点P