题目内容
已知平面向量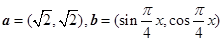
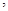 若函数
若函数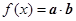 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图象上的所有的点向左平移1个单位长度,得到函数
的图象上的所有的点向左平移1个单位长度,得到函数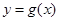 的图象,若函数
的图象,若函数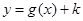 在
在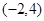 上有两个零点,求实数
上有两个零点,求实数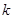 的取值范围.
的取值范围.
(Ⅰ)函数 的最小正周期为8.(Ⅱ)实数
的最小正周期为8.(Ⅱ)实数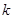 取值范围为
取值范围为 .
.
解析试题分析:(Ⅰ)根据平面向量的坐标运算公式,利用三角公式化简得到
 ,由
,由 ,得到最小正周期为8.(Ⅱ)通过将函数
,得到最小正周期为8.(Ⅱ)通过将函数 的图像向左平移1个单位后得到函数
的图像向左平移1个单位后得到函数 的表达式,结合函数的图象,建立
的表达式,结合函数的图象,建立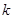 的不等式,确定得到实数
的不等式,确定得到实数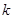 取值范围为
取值范围为 .
.
试题解析:解:(Ⅰ)∵ 函数
函数
∴ 1分
1分
 3分
3分
∴ ∴函数
∴函数 的最小正周期为8. 6分
的最小正周期为8. 6分
(Ⅱ)依题意将函数 的图像向左平移1个单位后得到函数
的图像向左平移1个单位后得到函数 8分
8分
函数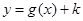 在
在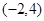 上有两个零点,即函数
上有两个零点,即函数 与
与 在
在 有两个交点,如图所示:
有两个交点,如图所示:
所以 ,即
,即
所以实数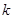 取值范围为
取值范围为 . 12分
. 12分
考点:1、平面向量的坐标运算,2、正弦型函数的图象和性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
数列 满足
满足 ,其中
,其中 ,设
,设 ,则
,则 等于( ).
等于( ).
A. | B. | C. | D. |
A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
(1)求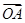 ·
·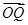 +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin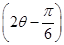 的值.
的值.
已知数列{an}满足a1=1,an+1= ,则其前6项之和是( )
,则其前6项之和是( )
| A.16 | B.20 | C.33 | D.120 |
 ,-1),b=
,-1),b=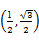 .
. ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线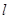 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线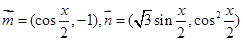 ,设函数
,设函数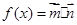
 在区间
在区间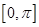 上的零点;
上的零点;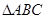 中,角
中,角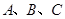 的对边分别是
的对边分别是 ,且满足
,且满足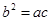 ,求
,求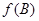 的取值范围.
的取值范围.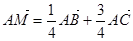 ,则
,则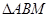 与
与 的面积之比为 .
的面积之比为 .