题目内容
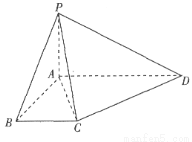
(本小题满分13分)如图,四棱锥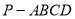 中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
(1)求三棱锥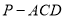 的外接球的体积;
的外接球的体积;
(2)求二面角 与二面角
与二面角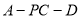 的正弦值之比.
的正弦值之比.
(1)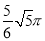 ;(2)
;(2)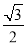 .
.
【解析】
试题分析:(1)由题意可知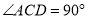 ,且
,且 平面
平面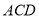 ,所以三棱锥
,所以三棱锥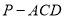 的外接球的球队心为
的外接球的球队心为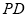 中点,又直径
中点,又直径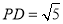 ,可求外接球体积;(2)建立空间直角坐标系,由空间向量求出二面角
,可求外接球体积;(2)建立空间直角坐标系,由空间向量求出二面角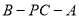 与二面角
与二面角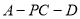 的的余弦值,再分别求出其正弦值即可.
的的余弦值,再分别求出其正弦值即可.
试题解析:(1)连接AC,则AC⊥CD,
又PA⊥平面ABCD,∴PA⊥CD,
∴CD⊥平面PAC,
又PC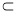 平面PAC,
平面PAC,
∴∠PCD=90°,(2分)
而∠PAD=90°,
从而三棱锥P-ACD外接球的球心为PD中点E.(4分)
直径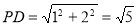 ,
,
所以三棱锥P-ACD外接球的体积
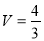
 .(6分)
.(6分)
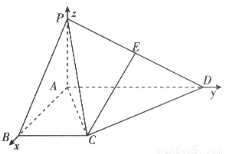
(2)建立坐标系,以点A为坐标原点,
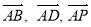 分别为
分别为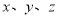 轴正方向,
轴正方向,
则B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,1)
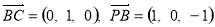 .
.
设平面PBC的法向量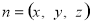 ,则
,则 即
即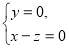
∴ =(1,0,1)
=(1,0,1)
由(1)知CD⊥平面PAC,故平面PAC的一个法向量为 =(-1,1,0),(8分)
=(-1,1,0),(8分)
所以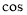
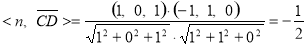 .
.
二面角B-PC-A的大小为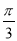 ,其正弦值为
,其正弦值为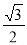 ,(10分)
,(10分)
由CD⊥平面PAC,得平面PCD⊥平面PAC,二面角A-PC-D为直二面角,其正弦值为1,(12分)
综上,二面角B—PC—A与二面角A—PC—D的正弦值之比为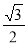 .(13分)
.(13分)
考点:空间线面垂直判定与性质、空间向量的应用.

练习册系列答案
相关题目
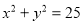
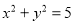
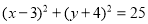
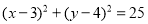
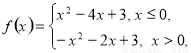 不等式
不等式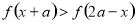 在
在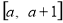 上恒成立,则实数
上恒成立,则实数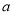 的取值范围是( )
的取值范围是( )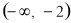 B.
B. 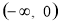 C.
C. 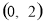 D.
D. 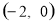
 ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
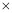 DN=____________.
DN=____________.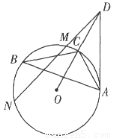
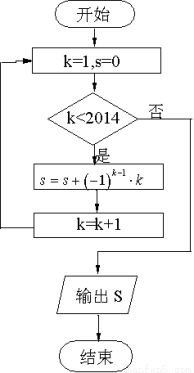
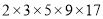 ”之值,则判断框内不能填入
”之值,则判断框内不能填入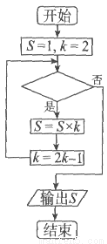
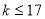 ? B.
? B. 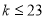 C.
C. 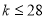 ? D.
? D. 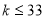 ?
?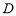 为
为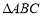 的边
的边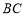 的中点,
的中点,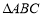 所在平面内有一个点
所在平面内有一个点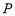 ,满足
,满足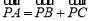 ,则
,则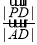 的值为
的值为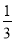 (B)
(B)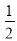
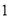 (D)
(D)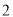
 ,
, ,则
,则 = .
= .