题目内容
11.设函数f(x)=x2+(a-2)x-1的单调递增区间为[2,+∞),则实数a的取值集合为[-2,+∞).分析 根据一元二次函数单调性的性质进行求解即可.
解答 解:若f(x)=x2+(a-2)x-1的单调递增区间为[2,+∞),
则满足对称轴x=$-\frac{a-2}{2}$≤2,
即a≥-2,
即实数a的取值集合为[-2,+∞),
故答案为:[-2,+∞).
点评 本题主要考查一元二次函数单调性的应用,确定对称轴和区间的关系是解决本题的关键.

练习册系列答案
相关题目
6.设f(x)=3x+3x-8,现用二分法求方程3x+3x-8=0在区间(1,2)内的近似解的,计算得f(1)<0,f(1.25)<0,f(1.5)>0,f(2)>0,则方程的根落在的区间( )
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |

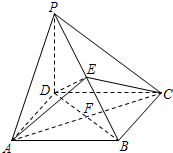 如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD;四边形ABCD是菱形,经过AC作与PD平行的平面交PB与点E,ABCD的两对角线交点为F.求证:AC⊥DE.