题目内容
20.已知函数f(x)=$\frac{1+lnx}{x}$.(1)求函数f(x)的单调区间和极值;
(2)若对任意的x∈(0,+∞),不等式lnx≤kx2-1恒成立,求实数k的取值范围.
分析 (1)先求导,根据导数和函数单调性的关系即可求出单调区间和极值;
(2)对于恒成立的问题,分离参数,构造函数,利用导数求出函数的最值.
解答 解:(1)∵f(x)=$\frac{1+lnx}{x}$,x>0,
∴f′(x)=$\frac{1-1-lnx}{{x}^{2}}$=-$\frac{lnx}{{x}^{2}}$,
令f′(x)=0,解得x=1,
当x>1时,f′(x)<0,函数单调减,
当0<x<1时,f′(x)>0,函数单调增,
∴f(x)在(0,1)上为增函数,在(1,+∞)为减函数,
当x=1函数有极大值,极大值为f(1)=1,无极小值;
(2)任意的x∈(0,+∞),不等式lnx≤kx2-1恒成立,
∴k≥$\frac{1+lnx}{{x}^{2}}$在(0,+∞)上恒成立,
设g(x)=$\frac{1+lnx}{{x}^{2}}$,
∴g′(x)=$\frac{-1-2lnx}{{x}^{3}}$,
令g′(x)=0,解得x=$\frac{1}{\sqrt{e}}$,
当x>$\frac{1}{\sqrt{e}}$时,f′(x)<0,函数单调减,
当0<x<$\frac{1}{\sqrt{e}}$时,f′(x)>0,函数单调增,
∴g(x)max=g($\frac{1}{\sqrt{e}}$)=$\frac{e}{2}$,
∴k≥$\frac{e}{2}$,
∴实数k的取值范围[$\frac{e}{2}$,+∞).
点评 本题考查了恒成立的问题,熟练掌握利用导数研究函数的单调性、极值与最值、等价转化的方法等是解题的关键,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
10.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=ex | B. | y=cosx | C. | y=|x|+1 | D. | y=$\sqrt{x}$ |
8.已知函数f(x)=$\left\{\begin{array}{l}-x+m\\-(m+4)x+{m^2}-m-3\end{array}$$\begin{array}{l},x≥0\\;x<0\end{array}$,若对任意的实数x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$<0,则实数m的取值范围是( )
| A. | (-4,+∞) | B. | (-∞,-1)∪(3,+∞) | C. | (-∞,-1]∪[3,+∞) | D. | (-4,-1]∪[3,+∞) |
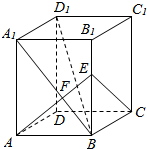 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.