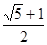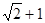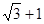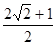题目内容
椭圆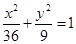 的弦被点
的弦被点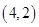 平分,则此弦所在的直线方程是( )
平分,则此弦所在的直线方程是( )
A.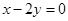 | B.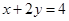 | C.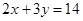 | D.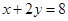 |
D
解析试题分析:由题意可设该弦所在直线的斜率为 ,若
,若 不存在则不合题意,则可设该所在的直线方程为
不存在则不合题意,则可设该所在的直线方程为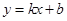 ,直线与椭圆的交点为
,直线与椭圆的交点为 、
、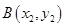 ,则
,则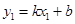 、
、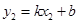 ,
, ,
, ,又
,又 ,
,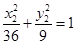 ,两式作差化简得
,两式作差化简得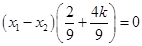 ,当
,当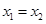 时直线与
时直线与 轴平行,不合题意,所以有
轴平行,不合题意,所以有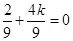 ,解得
,解得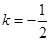 ,由点斜式可求得该弦所在直线方程为
,由点斜式可求得该弦所在直线方程为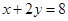 ,所以正确答案为D.
,所以正确答案为D.
考点:直线与椭圆关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点 是抛物线
是抛物线 的焦点,点
的焦点,点 在该抛物线上,且点
在该抛物线上,且点 的横坐标是
的横坐标是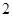 ,则
,则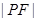 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
双曲线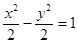 的渐近线方程为( )
的渐近线方程为( )
A.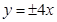 | B.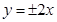 | C.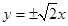 | D.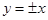 |
若双曲线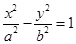 的离心率为
的离心率为 ,则其渐近线的斜率为( )
,则其渐近线的斜率为( )
A. | B.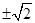 | C. | D.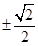 |
已知圆 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线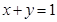 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )
A.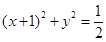 | B.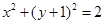 |
C.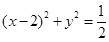 | D. |
已知双曲线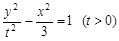 的一个焦点与抛物线
的一个焦点与抛物线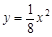 的焦点重合,则此双曲线的离心率为( )
的焦点重合,则此双曲线的离心率为( )
| A.2 | B.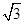 | C.3 | D.4 |
已知双曲线 的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
的左焦点为F1,左、右顶点分别为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为( )
| A.相交 | B.相切 | C.相离 | D.以上情况都有可能 |
已知抛物线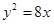 的焦点与双曲线
的焦点与双曲线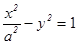 的一个焦点重合,则该双曲线的离心率为( )
的一个焦点重合,则该双曲线的离心率为( )
A.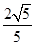 | B.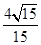 | C. | D.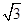 |
 有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( )
有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( )