Question

5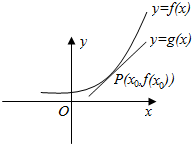．已知可导函数y=f（x）在点P（x₀，f（x₀））处切线为l：y=g（x）（如图），设F（x）=f（x）-g（x），则（　　）

• A． F′（x₀）=0，x=x₀是F（x）的极大值点
• B． F′（x₀）=0，x=x₀是F（x）的极小值点
• C． F′（x₀）≠0，x=x₀不是F（x）的极值点
• D． F′（x₀）≠0，x=x₀是F（x）的极值点

Answer 1

分析 由F（x）=f（x）-g（x）在x₀处先减后增，得到F′（x₀）=0，x=x₀是F（x）的极小值点．

解答 解：∵可导函数y=f（x）在点P（x₀，f（x₀））处切线为l：y=g（x），
∴F（x）=f（x）-g（x）在x₀处先减后增，
∴F′（x₀）=0，
x=x₀是F（x）的极小值点．
故选B．

点评 本题考查函数在某点取得极值的条件的应用，是中档题．解题时要认真审题，仔细解答，注意合理地进行等价转化．