题目内容
16．已知角α终边上一点P（2，-$\sqrt{5}$），则sinα等于（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{\sqrt{5}}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |
分析 根据三角函数的定义，首先求出P到原点的距离，然后利用sinα=$\frac{y}{r}$求之．
解答 解：由题意，P到原点的距离为：$\sqrt{{2}^{2}+（-\sqrt{5}）^{2}}$=3，所以sinα=$\frac{-\sqrt{5}}{3}$；
故选：B．
点评 本题考查了利用三角函数的定义求三角函数值；关键是熟练掌握三角函数的坐标法定义．
练习册系列答案
相关题目
11．{an}是首项a1=1，公差d=3的等差数列，若an=2014，则序号n的值为（ ）
| A． | 670 | B． | 672 | C． | 674 | D． | 668 |
1．下列说法正确的是（ ）
| A． | 命题“若xy=0，则x=0或y=0”的否命题为“若xy≠0，则x≠0或y≠0” | |
| B． | 若命题p为假命题，命题￢q为真命题，则命题“p∨q”为真命题 | |
| C． | “$\frac{a}{b}$＞1”是“a＞b＞0”的必要不充分条件 | |
| D． | 命题“任意x＞1，x+1＞2”的否定是“存在x≤1，x+1≤2” |
5．
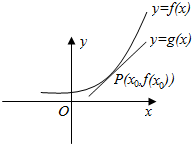已知可导函数y=f（x）在点P（x0，f（x0））处切线为l：y=g（x）（如图），设F（x）=f（x）-g（x），则（ ）
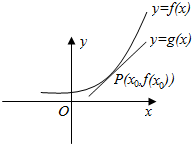已知可导函数y=f（x）在点P（x0，f（x0））处切线为l：y=g（x）（如图），设F（x）=f（x）-g（x），则（ ）| A． | F′（x0）=0，x=x0是F（x）的极大值点 | B． | F′（x0）=0，x=x0是F（x）的极小值点 | ||
| C． | F′（x0）≠0，x=x0不是F（x）的极值点 | D． | F′（x0）≠0，x=x0是F（x）的极值点 |