题目内容
已知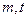 是实数,
是实数,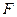 是抛物线
是抛物线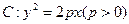 的焦点,直线
的焦点,直线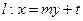 .
.
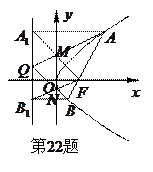 (1)若
(1)若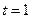 ,且
,且 在直线
在直线 上,求抛物线
上,求抛物线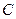 的方程;
的方程;
(2)当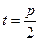 时,设直线
时,设直线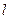 与抛物线
与抛物线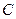 交于
交于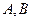 两点,过
两点,过
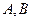 分别作抛物线
分别作抛物线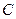 的准线的垂线,垂足为
的准线的垂线,垂足为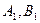 ,连
,连
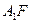 交
交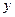 轴于点
轴于点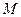 ,连结
,连结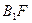 交
交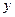 轴于点
轴于点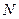 .
.
①证明: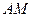 ⊥
⊥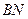 ;
;
②若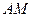 与
与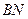 交于点
交于点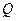 ,记△
,记△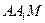 、四边形
、四边形
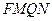 、△
、△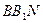 的面积分别为
的面积分别为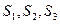 ,问
,问
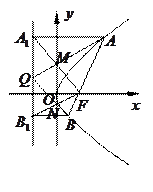 是否存在实数
是否存在实数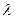 ,使
,使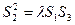 成立?若存在,求出
成立?若存在,求出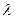 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 是实数,
是实数,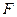 是抛物线
是抛物线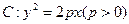 的焦点,直线
的焦点,直线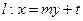 .
.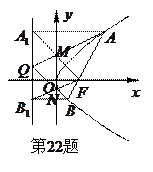 (1)若
(1)若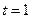 ,且
,且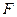 在直线
在直线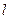 上,求抛物线
上,求抛物线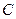 的方程;
的方程;(2)当
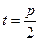 时,设直线
时,设直线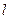 与抛物线
与抛物线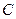 交于
交于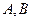 两点,过
两点,过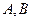 分别作抛物线
分别作抛物线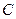 的准线的垂线,垂足为
的准线的垂线,垂足为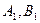 ,连
,连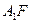 交
交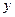 轴于点
轴于点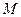 ,连结
,连结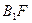 交
交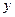 轴于点
轴于点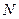 .
.①证明:
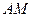 ⊥
⊥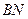 ;
;②若
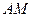 与
与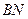 交于点
交于点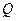 ,记△
,记△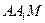 、四边形
、四边形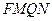 、△
、△ 的面积分别为
的面积分别为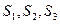 ,问
,问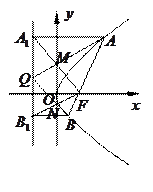 是否存在实数
是否存在实数 ,使
,使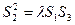 成立?若存在,求出
成立?若存在,求出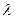 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.解:(1)当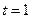 时,直线
时,直线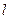 过定点
过定点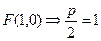 .
.
∴抛物线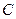 的方程是
的方程是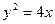 …………………………4分
…………………………4分
 (2)①设
(2)①设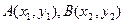 .联立
.联立 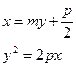 ,消去
,消去
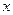 ,得
,得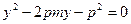 ,△
,△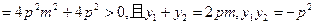 …6分
…6分
由已知,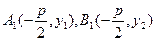 ,于是
,于是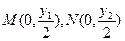
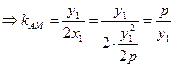
同理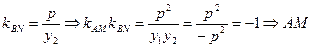 ⊥
⊥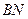 ……………………9分
……………………9分
①方法二:
由抛物线定义知,∵
又∵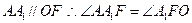 …………………5分
…………………5分
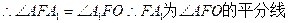 ……6分
……6分
同理FB1为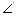 BFO的平分线,
BFO的平分线,
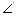 A1FB1=900 ……7分
A1FB1=900 ……7分
又等腰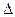 AA1F中,AM为中线,
AA1F中,AM为中线,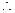 AM
AM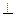 A1F
A1F
同理BN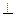 B1F ……………8分
B1F ……………8分
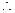
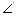 AQB=900即AM
AQB=900即AM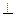 BN ……………9分
BN ……………9分
②因 ,所以,
,所以,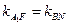 ,得
,得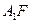 ∥
∥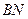 .同理,
.同理,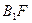 ∥
∥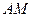 ,而
,而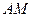 ⊥
⊥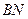 ,∴四边形
,∴四边形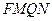 是一个矩形.……………………11分
是一个矩形.……………………11分
 ∴
∴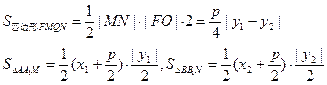 ,而
,而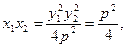
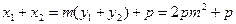 ……………………13分
……………………13分
假设存在实数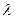 使
使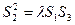 成立,则有
成立,则有
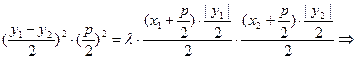
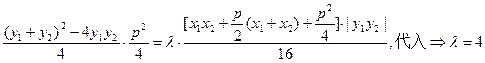 .
.
故存在实数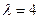 ,使
,使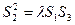 成立.…………15分
成立.…………15分
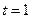 时,直线
时,直线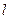 过定点
过定点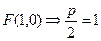 .
.∴抛物线
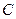 的方程是
的方程是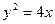 …………………………4分
…………………………4分 (2)①设
(2)①设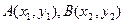 .联立
.联立 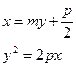 ,消去
,消去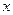 ,得
,得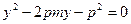 ,△
,△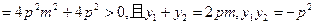 …6分
…6分由已知,
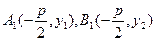 ,于是
,于是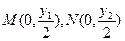
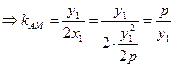
同理
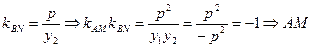 ⊥
⊥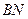 ……………………9分
……………………9分①方法二:
由抛物线定义知,∵

又∵
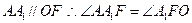 …………………5分
…………………5分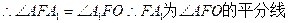 ……6分
……6分同理FB1为
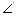 BFO的平分线,
BFO的平分线,
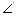 A1FB1=900 ……7分
A1FB1=900 ……7分 又等腰
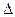 AA1F中,AM为中线,
AA1F中,AM为中线,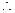 AM
AM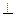 A1F
A1F同理BN
 B1F ……………8分
B1F ……………8分
 AQB=900即AM
AQB=900即AM BN ……………9分
BN ……………9分②因
 ,所以,
,所以,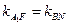 ,得
,得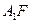 ∥
∥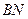 .同理,
.同理,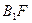 ∥
∥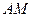 ,而
,而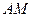 ⊥
⊥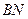 ,∴四边形
,∴四边形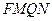 是一个矩形.……………………11分
是一个矩形.……………………11分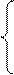 ∴
∴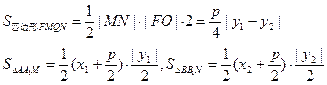 ,而
,而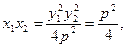
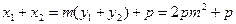 ……………………13分
……………………13分假设存在实数
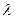 使
使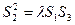 成立,则有
成立,则有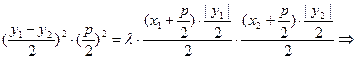
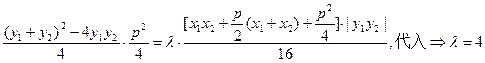 .
.故存在实数
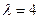 ,使
,使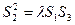 成立.…………15分
成立.…………15分略

练习册系列答案
相关题目
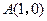 、
、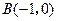 ,已知
,已知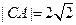 ,
,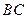 的垂直平分线
的垂直平分线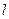 交
交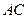 于
于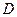 ,当点
,当点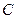 为动点时,点
为动点时,点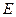 .
.
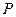 为
为 为坐标原点,曲线
为坐标原点,曲线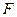 ,求
,求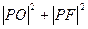 的最小值.
的最小值.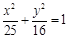 的离心率为
的离心率为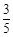
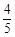
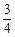
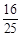
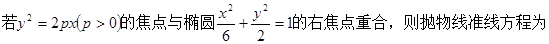 ( )
( )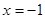
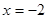
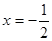
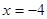
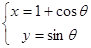 ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是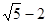
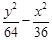 =1
=1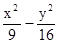 =1
=1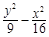 ="1"
="1" 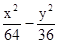 =1
=1 :
: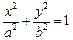 (
(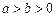 )过点
)过点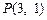 ,其左、右焦点分别为
,其左、右焦点分别为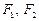 ,且
,且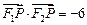 .
.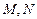 是直线
是直线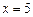 上的两个动点,且
上的两个动点,且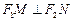 ,则以
,则以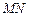 为直径的圆
为直径的圆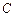 是否过定点?请说明理由.
是否过定点?请说明理由.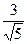 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.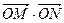 的值;
的值;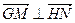 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.