题目内容
 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= ,BC=6.
,BC=6.
(Ⅰ)求证:BD⊥平面PAC;]
(Ⅱ)求二面角A-PC-D的余弦值.
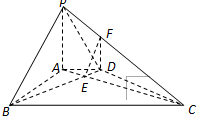 解法一:(Ⅰ)∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA.
解法一:(Ⅰ)∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA.又
 ,
,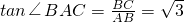 ,
,∴∠ABD=30,°∠BAC=60°
∴∠AEB=90°,即BD⊥AC
又PA∩AC=A,
∴BD⊥平面PAC.
(Ⅱ)过E作EF⊥PC,垂足为F,连接DF,
∵DE⊥平面PAC,EF是DF在平面PAC上的射影,由三垂线定理知PC⊥DF,
∴∠EFD为二面角A-PC-D的平面角.
又∠DAC=90°-∠BAC=30°
∴DE=ADsin∠DAC=1,AE=ABsin∠ABE=
 ,
,又AC=
 ,
,∴EC=
 ,PC=8.
,PC=8.由Rt△EFC∽Rt△PAC得
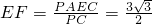
在Rt△EFD中,
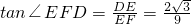 ,
,∴
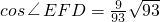 .
.∴二面角A-PC-D的余弦值为
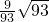 .
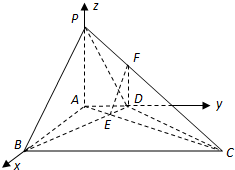
.解法二:(Ⅰ)如图,建立坐标系,则A(0,0,0),B(
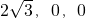 ),
),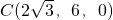 ,D(0,2,0),P(0,0,4)
,D(0,2,0),P(0,0,4)∴
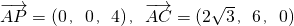 ,
,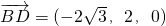
∴
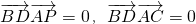 ,
,∴BD⊥AP,BD⊥AC,又PA∩AC=A
∴BD⊥平面PAC.
(Ⅱ)设平面PCD的法向量为
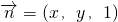 ,
,
则
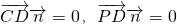 ,
,又
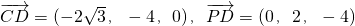 ,
,∴
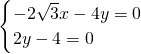 ,解得
,解得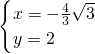
∴
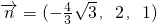
平面PAC的法向量取为
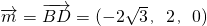
∴
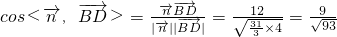 =
=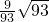
∴二面角A-PC-D的余弦值为
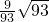 .
.分析:解法一:(Ⅰ)根据PA⊥平面ABCD,BD?平面ABCD,可得BD⊥PA.又可证BD⊥AC,利用线面垂直的判定定理,我们可证BD⊥平面PAC.
(Ⅱ)过E作EF⊥PC,垂足为F,连接DF,则∠EFD为二面角A-PC-D的平面角.在Rt△EFD中,我们可求二面角A-PC-D的余弦值为
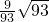 .
.解法二:(Ⅰ)建立空间坐标系,利用向量的数量积,我们可以证明BD⊥AP,BD⊥AC,利用线面垂直的判定定理,我们可证BD⊥平面PAC.
(Ⅱ)设平面PCD的法向量为
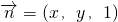 ,利用
,利用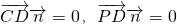 ,可得
,可得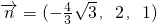 ,平面PAC的法向量取为
,平面PAC的法向量取为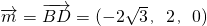 ,利用
,利用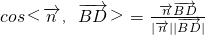 ,我们可求二面角A-PC-D的余弦值.
,我们可求二面角A-PC-D的余弦值.点评:本题以四棱锥为载体,考查线面垂直,考查面面角,采用两种解法,体现了一题多解,又体现了向量解法的优越性.

练习册系列答案
相关题目
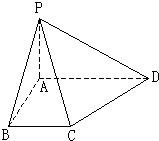 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且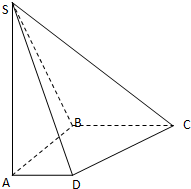 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=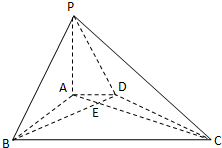 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=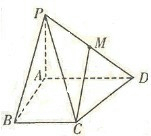 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点. 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.