题目内容
已知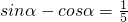 ,且0<α<π,求
,且0<α<π,求
(1)sinαcosα; (2)sinα+cosα.
解:(1)∵sinα-cosα= ,等式两边分别平方得:
,等式两边分别平方得:
sin2α-2sinα•cosα+cos2α= ,
,
即1-2sinα•cosα= ,
,
∴sinαcosα= ;
;
(2)∵sinαcosα= >0,
>0,
∵0<α<π,sinα>0,
∴cosα>0,
∴0<α< ;
;
∴(sinα+cosα)2=1+sin2α=1+ =
= ,
,
∴sinα+cosα= .
.
分析:由sinα-cosα= ,0<α<π,可得0<α<
,0<α<π,可得0<α< ,从而可得sinα+cosα=
,从而可得sinα+cosα= .
.
点评:本题考查三角函数中的恒等变换应用,关键在于理清三角函数间的关系,合理恰当的运用三角函数公式解决问题,属于中档题.
 ,等式两边分别平方得:
,等式两边分别平方得:sin2α-2sinα•cosα+cos2α=
 ,
,即1-2sinα•cosα=
 ,
,∴sinαcosα=
 ;
;(2)∵sinαcosα=
 >0,
>0,∵0<α<π,sinα>0,
∴cosα>0,
∴0<α<
 ;
;∴(sinα+cosα)2=1+sin2α=1+
 =
= ,
,∴sinα+cosα=
 .
.分析:由sinα-cosα=
 ,0<α<π,可得0<α<
,0<α<π,可得0<α< ,从而可得sinα+cosα=
,从而可得sinα+cosα= .
.点评:本题考查三角函数中的恒等变换应用,关键在于理清三角函数间的关系,合理恰当的运用三角函数公式解决问题,属于中档题.

练习册系列答案
相关题目
 ,②
,② =
=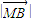 =
= ,③
,③ ∥
∥
 ,0),已知
,0),已知 ∥
∥ ,
, ∥
∥ 且
且 •
• =0.求四边形PRQN面积S的最大值和最小值.
=0.求四边形PRQN面积S的最大值和最小值. ,且0<θ<π,求函数f(x)=2sin(2x+θ)在区间
,且0<θ<π,求函数f(x)=2sin(2x+θ)在区间 上的最大值与最小值.
上的最大值与最小值.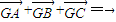 ,②
,②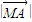 =
=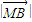 =
=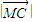 ,③
,③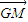 ∥
∥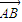
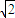 ,0),已知
,0),已知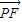 ∥
∥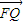 ,
,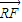 ∥
∥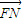 且
且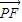 •
•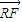 =0.求四边形PRQN面积S的最大值和最小值.
=0.求四边形PRQN面积S的最大值和最小值.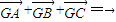 ,②
,② =
=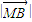 =
=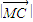 ,③
,③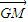 ∥
∥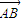
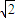 ,0),已知
,0),已知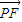 ∥
∥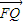 ,
,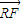 ∥
∥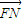 且
且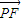 •
•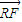 =0.求四边形PRQN面积S的最大值和最小值.
=0.求四边形PRQN面积S的最大值和最小值. ,且0<
,且0< <
< <
< .
. 的值;
的值;