题目内容
当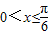 时,函数
时,函数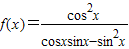 的最小值为 .
的最小值为 .
【答案】分析:化简函数的解析式为 ,求出tanx-tan2x 的最大值,从而得到
,求出tanx-tan2x 的最大值,从而得到 的最小值.
的最小值.
解答:解:函数 =
= .
.
∵ ,∴0<tanx≤
,∴0<tanx≤ ,∴tanx-tan2x>0.
,∴tanx-tan2x>0.
∴当tanx= 时,tanx-tan2x 有最大值为
时,tanx-tan2x 有最大值为 ,∴
,∴ 有最小值等于4.
有最小值等于4.
故答案为:4.
点评:本题主要考查同角三角函数的基本关系,正切函数的定义域和值域,二次函数的性质,化简函数的解析式为 ,是解题的突破口.
,是解题的突破口.
 ,求出tanx-tan2x 的最大值,从而得到
,求出tanx-tan2x 的最大值,从而得到 的最小值.
的最小值.解答:解:函数
 =
= .
.∵
 ,∴0<tanx≤
,∴0<tanx≤ ,∴tanx-tan2x>0.
,∴tanx-tan2x>0.∴当tanx=
 时,tanx-tan2x 有最大值为
时,tanx-tan2x 有最大值为 ,∴
,∴ 有最小值等于4.
有最小值等于4.故答案为:4.
点评:本题主要考查同角三角函数的基本关系,正切函数的定义域和值域,二次函数的性质,化简函数的解析式为
 ,是解题的突破口.
,是解题的突破口. 
练习册系列答案
相关题目
 则“
则“ ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件; 时,函数
时,函数 的最小值为2;
的最小值为2; ”与命题“
”与命题“ 或
或 ”都是真命题,则命题
”都是真命题,则命题 ,则
,则 .
.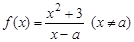 ,其中
,其中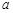 为非零常数.
为非零常数.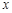 的不等式
的不等式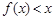 ;
; (Ⅱ)若当
(Ⅱ)若当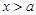 时,函数
时,函数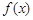 的最小值为3,求实数
的最小值为3,求实数 ,当
,当 时,函数
时,函数 的最小值为-4,则
的最小值为-4,则 的取值范围是________.
的取值范围是________. 的单调增区间是
的单调增区间是 .
. 的图象,需把函数
的图象,需把函数 的图象上所有点向左平行移动
的图象上所有点向左平行移动 个单位长度.
个单位长度. ,当
,当 时,函数
时,函数 的最小值为
的最小值为 .
. 、
、 、
、 是锐角
是锐角 的三个内角,则点
的三个内角,则点 在第四象限.
在第四象限.  时,函数
时,函数 的最小值为
的最小值为