题目内容
已知函数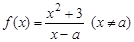 ,其中
,其中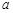 为非零常数.
为非零常数.
(Ⅰ)解关于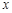 的不等式
的不等式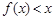 ;
; (Ⅱ)若当
(Ⅱ)若当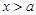 时,函数
时,函数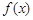 的最小值为3,求实数
的最小值为3,求实数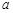 的值.
的值.
(Ⅰ)当 时,
时, ;当
;当 时,
时, 。(Ⅱ)
。(Ⅱ) 。
。
解析试题分析::(Ⅰ)不等式 即为
即为
当 时,不等式为
时,不等式为 ,不等式的解集为
,不等式的解集为
当 时,不等式为
时,不等式为 ,不等式的解集为
,不等式的解集为
 (Ⅱ)
(Ⅱ)

∵ ,∴
,∴ ≥
≥ ,当且仅当
,当且仅当 时取等号,
时取等号,
即 .
.
考点:本题考查分式不等式的解法、含参不等式的解法以及对号函数的最值问题。
点评:解含参数的不等式,常用的数学思想是分类讨论。分类讨论的主要依据是:①二次项系数的正负;②两根的大小;③判别式△的正负。

练习册系列答案
相关题目
 ,关于
,关于 的不等式
的不等式 的解集为
的解集为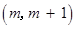 ,其中
,其中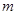 为非零常数.设
为非零常数.设 .
. 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且 ,求证:
,求证: N
N
 ,其中
,其中 为非零常数.
为非零常数. 的不等式
的不等式 ;
; 时,函数
时,函数 的最小值为3,求实数
的最小值为3,求实数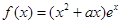 ,其中
,其中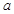 为正实数,
为正实数,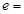 2.7182……
2.7182……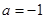 时,求
时,求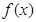 在点
在点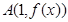 处的切线方程。
处的切线方程。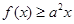 恒成立。
恒成立。