题目内容
在△ABC中,已知2 ·
· =
=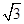 |
| |·|
|·| |=3|
|=3| |2,求角A,B,C的大小.
|2,求角A,B,C的大小.
 ·
· =
=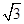 |
| |·|
|·| |=3|
|=3| |2,求角A,B,C的大小.
|2,求角A,B,C的大小.A= ,B=
,B= ,C=
,C= 或A=
或A= ,B=
,B= ,C=
,C=
 ,B=
,B= ,C=
,C= 或A=
或A= ,B=
,B= ,C=
,C=
解:设BC=a,AC=b,AB=c,
由2、 ·
· =
=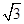 |
| |·|
|·| |得2bccosA=
|得2bccosA=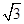 bc,
bc,
∴cosA=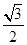 ,
,
又∵A∈(0,π),∴A= .
.
由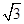 |
| |·|
|·| |=3|
|=3| |2得bc=
|2得bc=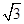 a2,
a2,
由正弦定理得
sinC·sinB=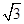 sin2A=
sin2A=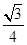 ,
,
∴sinC·sin(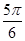 -C)=
-C)=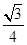 ,
,
即sinC·( cosC+
cosC+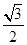 sinC)=
sinC)=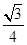 ,
,
∴2sinC·cosC+2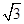 sin2C=
sin2C=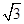 ,
,
∴sin2C-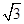 cos2C=0,
cos2C=0,
∴sin(2C-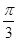 )=0,
)=0,
由A= 知0<C<
知0<C<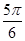 ,
,
∴-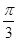 <2C-
<2C-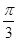 <
<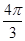 ,
,
从而2C-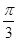 =0或2C-
=0或2C-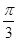 =π,
=π,
即C= 或C=
或C= .
.
故A= ,B=
,B= ,C=
,C= 或A=
或A= ,B=
,B= ,C=
,C= .
.
由2、
 ·
· =
=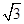 |
| |·|
|·| |得2bccosA=
|得2bccosA=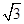 bc,
bc,∴cosA=
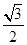 ,
,又∵A∈(0,π),∴A=
 .
.由
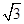 |
| |·|
|·| |=3|
|=3| |2得bc=
|2得bc=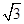 a2,
a2,由正弦定理得
sinC·sinB=
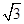 sin2A=
sin2A=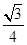 ,
,∴sinC·sin(
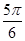 -C)=
-C)=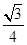 ,
,即sinC·(
 cosC+
cosC+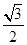 sinC)=
sinC)=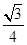 ,
,∴2sinC·cosC+2
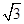 sin2C=
sin2C=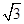 ,
,∴sin2C-
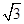 cos2C=0,
cos2C=0,∴sin(2C-
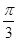 )=0,
)=0,由A=
 知0<C<
知0<C<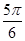 ,
,∴-
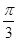 <2C-
<2C-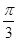 <
<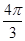 ,
,从而2C-
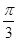 =0或2C-
=0或2C-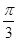 =π,
=π,即C=
 或C=
或C= .
.故A=
 ,B=
,B= ,C=
,C= 或A=
或A= ,B=
,B= ,C=
,C= .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 P是线段OM上一个动点.当
P是线段OM上一个动点.当 取最小值时,求
取最小值时,求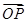 的坐标,并求
的坐标,并求 的值.
的值. 中,AB=3,AC=4,BC=5,AD⊥BC于D点,点
中,AB=3,AC=4,BC=5,AD⊥BC于D点,点 为
为 边所在直线上的一个动点,则
边所在直线上的一个动点,则 满足( ).
满足( ).
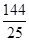
 ,则(2a-b)·b =( )
,则(2a-b)·b =( ) 的边长为2,
的边长为2, ,点
,点 分别在边
分别在边 上,
上, ,
, .若
.若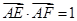 ,
,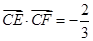 ,则
,则




 =2
=2 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则 ·
· 的值是( )
的值是( )


 .
. ,向量
,向量 ,则
,则 的最大值是
的最大值是