题目内容
如图,在正方体ABCD—A′B′C′D′中,AB=a.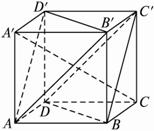
(1)求证:面AD′B′∥面C′DB;
(2)求证:A′C⊥面AD′B′;
(3)求平面AD′B′与面BC′D之间的距离.
(1)证明:∵D′B′∥BD,∴D′B′∥平面C′DB.?
同理,AB′∥平面C′DB.?
又D′B′∩AB′=B′,∴平面AD′B′∥平面C′DB.?
(2)证明:∵A′C′⊥B′D′,而A′C′为?A′C?在平面A′B′C′D′上的射影,∴A′C⊥面AD′B′.?
(3)解析:设A′C∩面AB′D′=M,A′C∩面BC′D=N,O′、O分别为上下底面的中心,则M∈AO′,N∈C′O,且AO′∥C′O.?
MN的长即为平面AD′B′与面C′DB的距离,即MN=A′M=NC=![]() A′C=
A′C=![]() a.
a.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )