题目内容
已知圆的方程x2+y2=25,点A为该圆上的动点,AB与x轴垂直,B为垂足,点P分有向线段BA的比λ=
.
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程.
| 3 | 2 |
(1)求点P的轨迹方程并化为标准方程形式;
(2)写出轨迹的焦点坐标和准线方程.
分析:(1)设出P点坐标和A点坐标,利用定比分点公式把A的坐标用P的坐标表示,代入圆的方程后可得点P的轨迹方程;
(2)由椭圆方程得到长半轴和短半轴,从而得到半焦距,则答案可求.
(2)由椭圆方程得到长半轴和短半轴,从而得到半焦距,则答案可求.
解答:解:(1)设点P(x,y)是轨迹上任意一点,点A的坐标是(x1,y1),点B的坐标是(x1,0),
∵点P分有向线段BA的比λ=
,
∴
,∴
,
又点A在圆x2+y2=25上,∴x2+
y2=25,
即
+
=1(y≠0);
(2)由椭圆
+
=1,知a2=25,b2=9,
∴c=4,则椭圆
+
=1的焦点坐标是(-4,0),(4,0),准线方程是x=±
=±
.
∵点P分有向线段BA的比λ=
| 3 |
| 2 |
∴
|
|
又点A在圆x2+y2=25上,∴x2+
| 25 |
| 9 |
即
| x2 |
| 25 |
| y2 |
| 9 |
(2)由椭圆
| x2 |
| 25 |
| y2 |
| 9 |
∴c=4,则椭圆
| x2 |
| 25 |
| y2 |
| 9 |
| a2 |
| c |
| 25 |
| 4 |
点评:本题考查了代入法求轨迹方程,训练了定必分点公式的用法,是中档题.

练习册系列答案
相关题目
已知圆的方程x2+y2=25,过M(-4,3)作直线MA,MB与圆交于点A,B,且MA,MB关于直线y=3对称,则直线AB的斜率等于( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知圆的方程x2+y2=4,若抛物线过点A(0,-1),B(0,1)且以圆的切线为准线,则抛物线的焦点轨迹方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
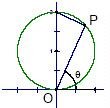 已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为
已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为