题目内容
已知函数 数列an的前n项和为Sn(n∈N*),点(n,Sn)均在函数y=f(x)的图象上,
数列an的前n项和为Sn(n∈N*),点(n,Sn)均在函数y=f(x)的图象上,(1)求数列an的通项公式an;
(2)令
 ,证明
,证明 .
.
【答案】分析:(1)点(n,Sn)均在函数y=f(x)的图象上,则sn= n2+
n2+ n,可得an=Sn-Sn-1=n+1,并验证a1即可;
n,可得an=Sn-Sn-1=n+1,并验证a1即可;
(2)证明:由cn=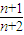 +
+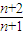 >2,得c1+c2+…+cn>2n;由cn=
>2,得c1+c2+…+cn>2n;由cn= +
+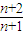 =2+
=2+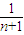 -
-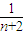 ,得c1+c2+…+cn=2n+(
,得c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+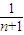 -
-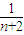 )=2n+
)=2n+ -
-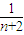 <2n+
<2n+ ;即证.
;即证.
解答:解:(1)∵点(n,Sn)均在函数y=f(x)的图象上,
∴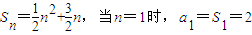 ,
,
当n≥2时,an=Sn-Sn-1=n+1,a1也适合,所以an=n+1(n∈N*).
(2)证明:∵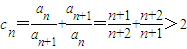 ,∴c1+c2+…+cn>2n;
,∴c1+c2+…+cn>2n;
又cn=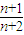 +
+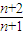 =2+
=2+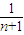 -
-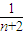 ,∴c1+c2+…+cn=2n+(
,∴c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+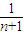 -
-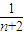 )=2n+
)=2n+ -
-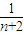 <2n+
<2n+ ;
;
∴2n<c1+c2+…+cn<2n+ .
.
点评:本题考查了数列与函数的综合应用问题,解题时运用了数列的前n项和求通项公式,应用基本不等式,拆项法等证明不等式成立,属于中档题.
 n2+
n2+ n,可得an=Sn-Sn-1=n+1,并验证a1即可;
n,可得an=Sn-Sn-1=n+1,并验证a1即可;(2)证明:由cn=
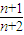 +
+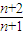 >2,得c1+c2+…+cn>2n;由cn=
>2,得c1+c2+…+cn>2n;由cn= +
+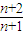 =2+
=2+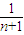 -
-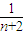 ,得c1+c2+…+cn=2n+(
,得c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+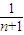 -
-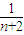 )=2n+
)=2n+ -
-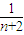 <2n+
<2n+ ;即证.
;即证.解答:解:(1)∵点(n,Sn)均在函数y=f(x)的图象上,
∴
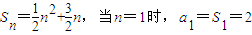 ,
,当n≥2时,an=Sn-Sn-1=n+1,a1也适合,所以an=n+1(n∈N*).
(2)证明:∵
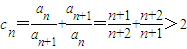 ,∴c1+c2+…+cn>2n;
,∴c1+c2+…+cn>2n;又cn=
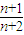 +
+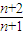 =2+
=2+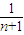 -
-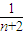 ,∴c1+c2+…+cn=2n+(
,∴c1+c2+…+cn=2n+( -
- +
+ -
- +…+
+…+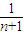 -
-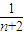 )=2n+
)=2n+ -
-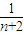 <2n+
<2n+ ;
;∴2n<c1+c2+…+cn<2n+
 .
.点评:本题考查了数列与函数的综合应用问题,解题时运用了数列的前n项和求通项公式,应用基本不等式,拆项法等证明不等式成立,属于中档题.

练习册系列答案
相关题目
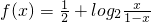 .
.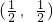 成中心对称;
成中心对称;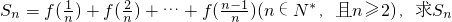 ;
;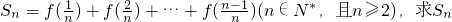 ,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.
,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围. .
.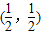 成中心对称;
成中心对称;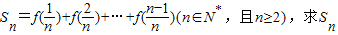 ;
;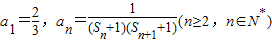 ,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.
,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.