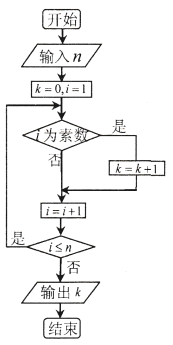
题目内容
【题目】已知椭圆![]() :
:![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,
,![]() 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接![]() 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交![]() 正半轴于
正半轴于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 的上方或重合).
的上方或重合).
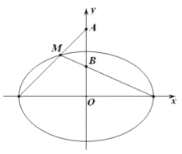
(1)当![]() 面积
面积![]() 最大时,求椭圆的方程;
最大时,求椭圆的方程;
(2)当![]() 时,若
时,若![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)当![]() 时,在
时,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值,若存在,求
为定值,若存在,求![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
【答案】(1) ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() ,使得
,使得![]() 为定值.
为定值.
【解析】
(1)由题意可得点A与点B重合时,![]() 面积最大,借助基本不等式即可求出b的值,可得椭圆方程;
面积最大,借助基本不等式即可求出b的值,可得椭圆方程;
(2)设出点![]() ,则
,则![]() :
:![]() ,
,![]() :
:![]() ,求出点A的坐标,点B的坐标,根据B是线段
,求出点A的坐标,点B的坐标,根据B是线段![]() 的中点,用中点坐标公式列方程,可得M点坐标,进而求出直线
的中点,用中点坐标公式列方程,可得M点坐标,进而求出直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() ,求出点A的坐标,根据向量的数量积即可求出
,求出点A的坐标,根据向量的数量积即可求出
解:(1)由已知:
![]()
![]() ,
,
当且仅当![]() 时等号成立;
时等号成立;
则:![]() ,
,
此时椭圆方程为: ;
;
(2)点![]() 在
在![]() 轴或其左侧,则图形如本题图,设
轴或其左侧,则图形如本题图,设![]() ,那么:
,那么:
![]() :
:![]() ,
,![]() :
:![]() ,
,
令![]()
得: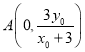 ,
,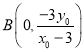 ,
,
![]() 是线段
是线段![]() 的中点,
的中点,
则:![]() ,
,
解得:![]() ,则
,则![]() ,
,
则:![]() :
:![]() ,即:
,即:![]() ;
;
(3)![]() :
:![]() ,设
,设![]() ,
,![]() ,
,
若点![]() 在
在![]() 轴左侧,则同上,
轴左侧,则同上,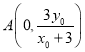 ,
,
![]() ,
,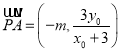 ,
,
![]()
![]()
![]() ,
,
此时,![]() ,
,![]() ;
;
综上,故存在点![]() 使得
使得![]() 为定值.
为定值.

【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取![]() 件产品作为样本称出它们的质量(单位:毫克),质量值落在
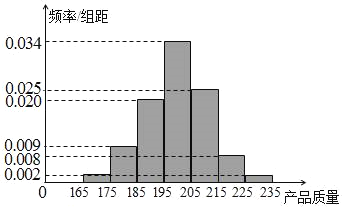
件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)以样本的频率作为概率,试估计从甲流水线上任取![]() 件产品,求其中不合格品的件数
件产品,求其中不合格品的件数![]() 的数学期望.
的数学期望.
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅱ)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
(Ⅲ)由乙流水线的频率分布直方图可以认为乙流水线生产的产品质量![]() 服从正态分布
服从正态分布![]() ,求质量
,求质量![]() 落在
落在![]() 上的概率.
上的概率.
参考公式:![]()
![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
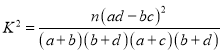 ,其中
,其中![]() .
.