题目内容
定义在(-1,1)上的函数f(x),对任意的x,y∈(-1,1)都有:f(x)+f(y)=f(
);且当x∈(-∞,0)时,f(x)>0,回答下列问题:
(1)判断函数f(x)在(-1,1)的奇偶性,并说明理由;
(2)判断函数f(x)在(-1,1)的单调性,并说明理由;
(3)若f(
)=
,试求f(
)-f(
)-f(
)的值.
| x+y |
| 1+xy |
(1)判断函数f(x)在(-1,1)的奇偶性,并说明理由;
(2)判断函数f(x)在(-1,1)的单调性,并说明理由;
(3)若f(
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 11 |
| 1 |
| 19 |
分析:(1)令x=y=0,y=-x,即可得出结论;
(2)利用函数单调性的证明步骤,可得结论;
(3)证明f(x)+f(-y)=f(x)-f(y)=f(
),代入计算,可得结论.
(2)利用函数单调性的证明步骤,可得结论;
(3)证明f(x)+f(-y)=f(x)-f(y)=f(
| x-y |
| 1-xy |
解答:解:(1)令x=y=0,则2f(0)=f(0),∴f(0)=0
令y=-x,∴f(0)=f(x)+f(-x)=0,∴f(-x)=-f(x)
∴f(x)是奇函数. …4
(2)任取x1,x2∈(-1,1)且设x1<x2
f(x1)-f(x2)=f(x1)+f(-x2)=f(
)
∵-1<x1<x2<1,∴x1-x2<0,则
<0
∴f(
)>0∴f(x1)>f(x2)
∴函数在给定区间上递减. …8
(3)f(x)+f(-y)=f(x)-f(y)=f(
)
∴f(
)-f(
)=f(
),f(
)-f(
)=f(
),f(
)-f(
)=f(
)
∴f(
)-f(
)-f(
)=2f(
)=1…12.
令y=-x,∴f(0)=f(x)+f(-x)=0,∴f(-x)=-f(x)
∴f(x)是奇函数. …4
(2)任取x1,x2∈(-1,1)且设x1<x2
f(x1)-f(x2)=f(x1)+f(-x2)=f(
| x1-x2 |
| 1-x1x2 |
∵-1<x1<x2<1,∴x1-x2<0,则
| x1-x2 |
| 1-x1x2 |
∴f(
| x1-x2 |
| 1-x1x2 |
∴函数在给定区间上递减. …8
(3)f(x)+f(-y)=f(x)-f(y)=f(
| x-y |
| 1-xy |
∴f(
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 11 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 19 |
| 1 |
| 5 |
∴f(
| 1 |
| 2 |
| 1 |
| 11 |
| 1 |
| 19 |
| 1 |
| 5 |
点评:本题考查函数的奇偶性、单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.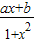 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.