题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:
为直径的圆经过坐标原点,证明:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)结合离心率![]() ,计算出a,b,c之间的关系,利用点到直线距离,计算a,b值,即可。(2)分直线AB斜率存在与不存在讨论,结合直线方程和椭圆方程,并利用
,计算出a,b,c之间的关系,利用点到直线距离,计算a,b值,即可。(2)分直线AB斜率存在与不存在讨论,结合直线方程和椭圆方程,并利用![]() ,计算O到直线距离,即可.
,计算O到直线距离,即可.
(1)∵椭圆![]() 的离心率
的离心率![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∵椭圆![]() 的左顶点
的左顶点![]() 到直线
到直线![]() ,即到
,即到![]() 的距离
的距离![]() ,
,
∴![]() ,
,
把![]() 代入得:
代入得:![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,
①当直线![]() 的斜率不存在时,由椭圆的性质可得:
的斜率不存在时,由椭圆的性质可得:![]() ,
,![]() ,
,
∵当直线![]() 的斜率不存在时,以
的斜率不存在时,以![]() 为直径的圆经过坐标原点,
为直径的圆经过坐标原点,
∴![]() ,即
,即![]() ,也就是
,也就是![]() ,
,
又∵点![]() 在椭圆
在椭圆![]() 上, ∴
上, ∴![]() ,
,
∵以![]() 为直径的圆经过坐标原点,且
为直径的圆经过坐标原点,且![]() 平行于
平行于![]() 轴,
轴,
∴![]() ,∴
,∴![]() ,解得:
,解得:![]()
此时点![]() 到直线
到直线![]() 的距离
的距离![]()
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
与椭圆方程联立有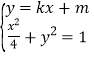 ,消去
,消去![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
同理: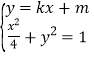 ,消去
,消去![]() ,得
,得![]() ,
,
即![]() ,∴
,∴![]()
∵![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,所以
,所以![]() ,∴
,∴![]()
∴![]()
∴![]()
∴![]()
∴点![]() 到直线
到直线![]() 的距离
的距离![]()
综上所述,点![]() 到直线
到直线![]() 的距离为定值
的距离为定值![]() .
.

练习册系列答案
相关题目