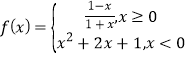题目内容
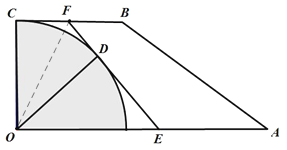
【题目】如图所示，直角梯形公园
中，
，
，
，公园的左下角阴影部分为以
为圆心，半径为
的
圆面的人工湖，现设计修建一条与圆相切的观光道路
（点
分别在
与
上），
为切点，设
.
（1）试求观光道路长度的最大值；
（2）公园计划在道路的右侧种植草坪，试求草坪
的面积最大值.
【答案】（1）
（2）
平方千米
【解析】
（1）求出
，分别求出
，
，从而求出
的表达式，求出的最大值即可；
（2）求出
的表达式，求出函数的导数，根据函数的单调性求出
的最大值即可．
解：（1）由题意可知
，
在
中，
，
在
中，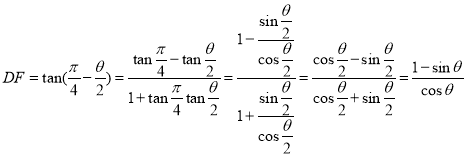
，
则
，
又因为，所以当
时，
，
此时，
故的最长值为；
（2）在中，
，由（1）得
，
则
则
，令
即
，解得
，
当
单调递增；当
单调递减，
所以为函数
的极大值，又函数在区间
极大值唯一，因此这个极大值也是函数的最大值.
，
所以草坪面积最大值为平方千米.
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
