题目内容
设等差数列{an}的前n项和为Sn,已知a3=12,S10>0,S13<0.
(1)求公差d的取值范围;
(2)若公差d∈Z,Sn为{an}的前n项和,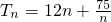 ,求证:对任意n∈N*,Sn<Tn.
,求证:对任意n∈N*,Sn<Tn.
解:(1)∵等差数列{an}中,a3=12,S10>0,S13<0,
∴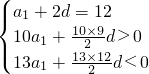 ,
,
解得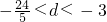 ,
,
∴公差d的取值范围是(- ,-3).
,-3).
(2)∵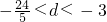 ,d∈Z,
,d∈Z,
∴d=-4,
∵a1+2d=12,
∴a1=20,
∴Sn=20n+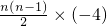 =-2n2+22n=-2(n-
=-2n2+22n=-2(n- )2+
)2+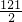 ,
,
∴n=5或n=6时,
(Sn)max=60,
又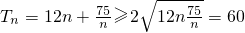 ,
,
即(Tn)min>60,
∴Sn<Tn.
分析:(1)等差数列{an}中,a3=12,S10>0,S13<0,故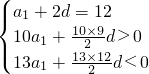 ,由此能求出公差d的取值范围.
,由此能求出公差d的取值范围.
(2)由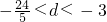 ,d∈Z,知d=-4,由a1+2d=12,知a1=20,故Sn=-2n2+22n=-2(n-
,d∈Z,知d=-4,由a1+2d=12,知a1=20,故Sn=-2n2+22n=-2(n- )2+
)2+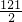 ,所以n=5或n=6时,(Sn)max=60,由
,所以n=5或n=6时,(Sn)max=60,由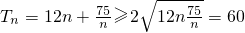 ,知Sn<Tn.
,知Sn<Tn.
点评:本题考查等差数列的通项公式和前n项和公式的应用,求等差数列的公差的取值范围,考查等差数列的最小值的求法和应用,解题时要认真审题,注意配方法和均值定理的灵活运用.
∴
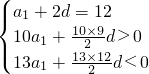 ,
,解得
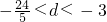 ,
,∴公差d的取值范围是(-
 ,-3).
,-3).(2)∵
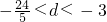 ,d∈Z,
,d∈Z,∴d=-4,
∵a1+2d=12,
∴a1=20,
∴Sn=20n+
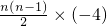 =-2n2+22n=-2(n-
=-2n2+22n=-2(n- )2+
)2+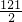 ,
,∴n=5或n=6时,
(Sn)max=60,
又
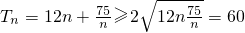 ,
,即(Tn)min>60,
∴Sn<Tn.
分析:(1)等差数列{an}中,a3=12,S10>0,S13<0,故
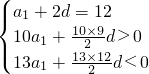 ,由此能求出公差d的取值范围.
,由此能求出公差d的取值范围.(2)由
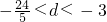 ,d∈Z,知d=-4,由a1+2d=12,知a1=20,故Sn=-2n2+22n=-2(n-
,d∈Z,知d=-4,由a1+2d=12,知a1=20,故Sn=-2n2+22n=-2(n- )2+
)2+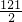 ,所以n=5或n=6时,(Sn)max=60,由
,所以n=5或n=6时,(Sn)max=60,由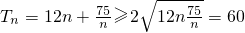 ,知Sn<Tn.
,知Sn<Tn.点评:本题考查等差数列的通项公式和前n项和公式的应用,求等差数列的公差的取值范围,考查等差数列的最小值的求法和应用,解题时要认真审题,注意配方法和均值定理的灵活运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目