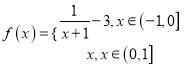题目内容
【题目】已知函数![]()
![]()
(1)若函数![]() 的图像在
的图像在![]() 处的切线
处的切线![]() 垂直于直线
垂直于直线![]() ,求实数
,求实数![]() 的值及直线
的值及直线![]() 的方程;
的方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:
,求证: ![]()
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)函数求导得![]() ,进而得切线方程;
,进而得切线方程;
(2)函数求导![]() ,讨论
,讨论![]() ,
, ![]() 两种情况;
两种情况;
(3)令![]() ,由
,由![]() 单调性,求最值即可证得.
单调性,求最值即可证得.
试题解析:
(1)![]()
![]() ,定义域为
,定义域为![]() ,
, ![]()
![]()
![]() 函数
函数![]() 的图像在
的图像在![]() 处的切线
处的切线![]() 的斜率
的斜率![]()
![]() 切线
切线![]() 垂直于直线
垂直于直线![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
, ![]() 切点为
切点为![]()
![]() 切线
切线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
(2)由(1)知: ![]() ,
, ![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, 
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]()
此时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是 ![]()
综上所述:
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是 ![]() 。
。
(3)由(2)知:当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
![]()
![]() 时,
时, ![]()
![]()
![]() 时,
时, ![]() ,即
,即![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
优 秀 | 不优秀 | |
甲 班 | 10 | 35 |
乙 班 | 7 | 38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
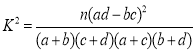
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |