Question

【题目】新高考取消文理科，实行“”模式，成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况，随机调查50人，并把调查结果制成下表：

年龄（岁）
频数	5	15	10	10	5	5
了解	4	12	6	5	2	1

（1）把年龄在称为中青年，年龄在称为中老年，请根据上表完成列联表，是否有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关？

	了解新高考	不了解新高考	总计
中青年
中老年
总计

附：.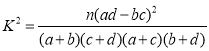

	0.050	0.010	0.001
	3.841	6.635	10.828

（2）若从年龄在的被调查者中随机选取3人进行调查，记选中的3人中了解新高考的人数为，求的分布列以及.

Answer 1

【答案】（1）填表见解析；有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关联（2）详见解析

【解析】

（1）根据数据列出列联表，求出的观测值，对照表格，即可得出结论；

（2）年龄在的被调查者共5人，其中了解新高考的有2人，可能取值为0，1，2，分别求出概率，列出随机变量分布列，根据期望公式即可求解.

解析：（1）列联表如图所示，

	了解新高考	不了解新高考	总计
中青年	22	8	30
中老年	8	12	20
总计	30	20	50

，

所以有95%的把握判断对新高考的了解与年龄（中青年、中老年）有关联.

（2）年龄在的被调查者共5人，其中了解新高考的有2人，

则抽取的3人中了解新高考的人数可能取值为0，1，2，

，

.

所以的分布列为

	0	1	2

.