题目内容
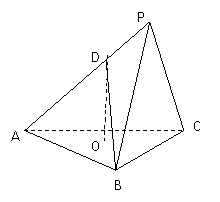 三棱锥
三棱锥![]() ,底面
,底面![]() 为边长为
为边长为![]() 的正三角形,平面
的正三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 为底面三角形中心.
为底面三角形中心.
(Ⅰ)求证:![]() ∥面
∥面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求平面![]() 截三棱锥
截三棱锥![]() 所得的较大几何体的体积.
所得的较大几何体的体积.
证明:(Ⅰ)连结![]() 并延长交
并延长交![]() 于点
于点![]() ,
,
连结![]() 、
、![]() . --------------1分
. --------------1分
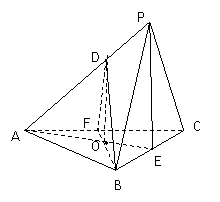
![]() 为正三角形
为正三角形![]() 的中心,
的中心,
∴![]() ,
,
又![]() , ∴
, ∴![]() ∥
∥![]() , --------------2分
, --------------2分
![]() 平面
平面![]() ,
,![]() 平面
平面![]() --------------3分
--------------3分
∴![]() ∥面
∥面![]() . --------------4分
. --------------4分
(Ⅱ)![]() ,且
,且![]() 为
为![]() 中点, ∴
中点, ∴![]() ,
,
又平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() . --------------5分
. --------------5分
由(Ⅰ)知,![]() ∥
∥![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() --------------6分
--------------6分
连结![]() ,则
,则![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() , --------------7分
, --------------7分
∴![]() . --------------8分
. --------------8分
(Ⅲ)连结![]() 并延长交
并延长交![]() 于点
于点![]() ,连结
,连结![]() ,则面
,则面![]() 将三棱锥
将三棱锥![]() 截成三棱锥
截成三棱锥![]() 和四棱锥
和四棱锥![]() 两个几何体 . --------------9分
两个几何体 . --------------9分
![]() -----------10分
-----------10分
![]() --------------11分
--------------11分
∴所截较大部分几何体的体积为![]() .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 已知正三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
已知正三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为 (2013•肇庆一模)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•肇庆一模)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )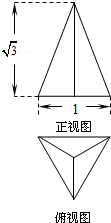 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) B.
B. C.
C. D.
D.