题目内容
【题目】已知函数![]() .
.
(![]() )若曲线
)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值.
的值.
(![]() )在(1)的条件下,求函数
)在(1)的条件下,求函数![]() 的单调区间和极值.
的单调区间和极值.
(![]() )在(1)的条件下,试判断函数
)在(1)的条件下,试判断函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
【答案】(![]() )
)![]() .(
.(![]() )单调递减区间
)单调递减区间![]() ,单调递减区间
,单调递减区间![]() ,极大值为
,极大值为![]() .(
.(![]() )
)![]() 个.
个.
【解析】试题分析:(1)欲求a的值,根据在点(1,f(1))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.再列出一个等式,最后解方程组即可得.
(2)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,最后求出极值即可.
(![]() )将
)将![]() 的零点个数问题转化为函数
的零点个数问题转化为函数![]() 与函数y
与函数y![]() 的交点个数问题,画出两个函数图象的草图,可知
的交点个数问题,画出两个函数图象的草图,可知![]() 与
与![]() 有两个交点.即
有两个交点.即![]() 有
有![]() 个零点.
个零点.
试题解析:(![]() )∵
)∵![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() .
.
(![]() )∵
)∵![]() ,
,
![]() ,令
,令![]() ,
,![]() ,
,
|
|
|
|
|
|
|
|
|
| 极大值 |
|
∴![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
![]() 极大值为
极大值为![]() .
.
(![]() )∵
)∵![]() ,
,
当![]() 时,即为
时,即为![]() ,
,
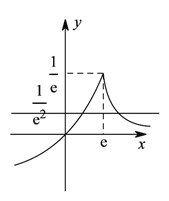
由(![]() )作出
)作出![]() 大致图象,
大致图象,
由图可知![]() 与
与![]() 有两个交点.
有两个交点.
即![]() 有
有![]() 个零点.
个零点.

练习册系列答案
相关题目