Question

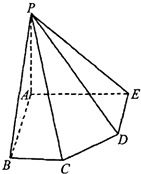
在五棱锥P—ABCDE中，PA=AB=AE=2a，PB=PE=2a，BC=DE=a，∠EAB=∠ABC=

∠DEA=90°.

（1）求证：PA⊥平面ABCDE；

（2）求二面角A—PD—E的余弦值.

Answer 1

(1) 证明略(2) 二面角A—PD—E的余弦值是.

解析:

（1）以A点为坐标原点，以AB、AE、AP所在直线分别为x、y、z轴，建立空间直角坐标系A—xyz，则由已知得

A（0，0，0），P（0，0，2a），

B（2a，0，0），C（2a，a，0），

D（a，2a，0），E（0，2a，0）.

∴=（0，0，2a），=（2a，0，0），=（0，2a，0），

∴·=0·2a+0·0+2a·0=0，

∴⊥.同理⊥.

又∵AB∩AE=A，∴PA⊥平面ABCDE.

（2）设平面PAD的法向量为m=(1,y,z),

则m·=0，得a+2ay=0，∴y=-.

又m·=0，得2az=0，∴z=0.

∴m=（1，-，0）.

再设平面PDE的法向量为n=(x,1,z),

而=（a，0，0），=（a，2a，-2a），

则n·=0，得ax=0，∴x=0.

又n·=0，得ax+2a-2az=0，∴z=1.

∴n=（0，1，1）.

令二面角A—PD—E的平面角为，

则cos=-==，

故二面角A—PD—E的余弦值是.