题目内容
已知f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
解析:把f(3)用f(1),f(2)表示.
∵f(x)=ax2-c,不妨设f(3)=mf(1)+nf(2),
∴
∴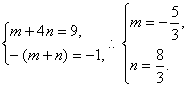
∴f(3)=![]() f(1)+
f(1)+![]() f(2).
f(2).
又∵-4≤f(1)≤-1,-1≤f(2)≤5,
∴-1≤f(3)≤20.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
已知f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
解析:把f(3)用f(1),f(2)表示.
∵f(x)=ax2-c,不妨设f(3)=mf(1)+nf(2),
∴
∴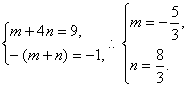
∴f(3)=![]() f(1)+
f(1)+![]() f(2).
f(2).
又∵-4≤f(1)≤-1,-1≤f(2)≤5,
∴-1≤f(3)≤20.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案