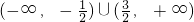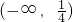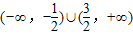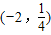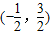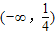Question

不等式3•4^x+8（a-a²）•2^x+8（a-a²）+9＞0对一切x∈R恒成立，则实数a的取值范围为（　　）

• A、(-∞，-

  1

  2

  )∪(

  3

  2

  ，+∞)
• B、(-2，

  1

  4

  )
• C、(-

  1

  2

  ，

  3

  2

  )
• D、(-∞，

  1

  4

  )

Answer 1

分析：利用换元令t=2^x，将不等式转化为二次不等式对一切t＞0恒成立，进而转化为△＜0，从而利用解不等式求出参数的范围．

解答：解：令t=2^x（t＞0），则问题转化为不等式3•t²+8（a-a²）•t+8（a-a²）+9＞0对一切t＞0恒成立，
故有△＜0，解得-

3

4

＜a-a2＜

9

4

，即-

1

2

＜a＜

3

2

，
故选C．

点评：本题求解的关键是利用换元将问题进行等价转化，利用二次不等式恒成立处理的方法求解，应注意转化的等价性．