题目内容
已知在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足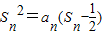 .
.(Ⅰ) 求Sn的表达式;
(Ⅱ) 设
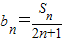 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】分析:(Ⅰ)当n≥2时,把an=Sn-Sn-1代入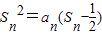 即可得到2SnSn-1+Sn-Sn-1=0,然后化简得
即可得到2SnSn-1+Sn-Sn-1=0,然后化简得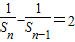 ,于是可以得到Sn的表达式,
,于是可以得到Sn的表达式,
(Ⅱ)把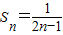 代入
代入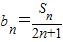 中可得bn=
中可得bn=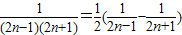 ,然后进行裂项相消进行求和.
,然后进行裂项相消进行求和.
解答:解:(Ⅰ)当n≥2时,an=Sn-Sn-1代入得: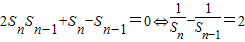 ,
,
∴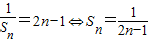 (6分)
(6分)
(Ⅱ)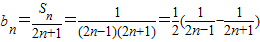
∴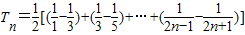 =
=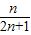 .(13分)
.(13分)
点评:本题主要考查数列的求和和求数列递推式的知识点,利用裂项相消法求数列的和是解答本题第二问的关键,本题难度一般.
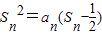 即可得到2SnSn-1+Sn-Sn-1=0,然后化简得
即可得到2SnSn-1+Sn-Sn-1=0,然后化简得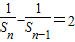 ,于是可以得到Sn的表达式,
,于是可以得到Sn的表达式,(Ⅱ)把
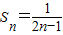 代入
代入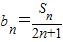 中可得bn=
中可得bn=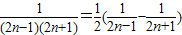 ,然后进行裂项相消进行求和.
,然后进行裂项相消进行求和.解答:解:(Ⅰ)当n≥2时,an=Sn-Sn-1代入得:
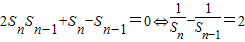 ,
,∴
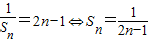 (6分)
(6分)(Ⅱ)
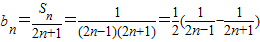
∴
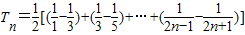 =
=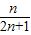 .(13分)
.(13分)点评:本题主要考查数列的求和和求数列递推式的知识点,利用裂项相消法求数列的和是解答本题第二问的关键,本题难度一般.

练习册系列答案
相关题目