题目内容
抛物线的顶点是椭圆16x2+25y2=400的中心,而焦点是椭圆的右焦点,求此抛物线的方程.
椭圆方程可化为
+
=1,
∵c2=25-16=9,c=3,
故中心(0,0),右焦点为(3,0).
设抛物线的方程为y2=2px(p>0),
则
=3,故p=6,
所以抛物线方程为y2=12x.
| x2 |
| 25 |
| y2 |
| 16 |
∵c2=25-16=9,c=3,
故中心(0,0),右焦点为(3,0).
设抛物线的方程为y2=2px(p>0),
则
| p |
| 2 |
所以抛物线方程为y2=12x.

练习册系列答案
相关题目
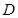 的顶点是椭圆
的顶点是椭圆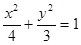 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.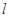 过点
过点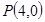 ,交抛物线
,交抛物线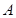 、
、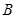 两点.
两点.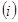 若直线
若直线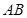 的长;
的长;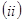 是否存在垂直于
是否存在垂直于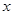 轴的直线
轴的直线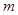 被以
被以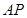 为直径的圆
为直径的圆 所截得的弦长恒为定值?如果存在,求出
所截得的弦长恒为定值?如果存在,求出 +
+ =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合.