题目内容
设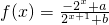 (a,b为实常数).
(a,b为实常数).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)求(2)中函数f(x)的值域.
解:(1)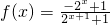 ,
,
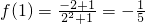 ,
,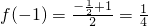 ,
,
所以f(-1)≠-f(1),f(x)不是奇函数;
(2)f(x)是奇函数时,f(-x)=-f(x),
即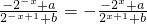 对任意实数x成立,
对任意实数x成立,
化简整理得(2a-b)•22x+(2ab-4)•2x+(2a-b)=0,这是关于x的恒等式,
所以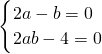 所以
所以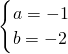 或
或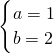 ;
;
(3) ,因为2x>0,所以2x+1>1,
,因为2x>0,所以2x+1>1, ,
,
从而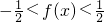 ;所以函数f(x)的值域为
;所以函数f(x)的值域为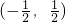 .
.
分析:(1)证明不是奇函数,可用特殊值法;如证明:f(-1)≠-f(1),f(x)不是奇函数;
(2)利用奇函数定义f(-x)=-f(x),再用待定系数法求解;
(3)先将原函数式化成: ,将2x看成整体,利用其范围结合不等式的性质即可求得函数f(x)的值域.
,将2x看成整体,利用其范围结合不等式的性质即可求得函数f(x)的值域.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查转化思想.属于基础题.
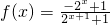 ,
,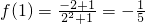 ,
,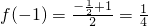 ,
,所以f(-1)≠-f(1),f(x)不是奇函数;
(2)f(x)是奇函数时,f(-x)=-f(x),
即
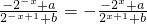 对任意实数x成立,
对任意实数x成立,化简整理得(2a-b)•22x+(2ab-4)•2x+(2a-b)=0,这是关于x的恒等式,
所以
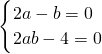 所以
所以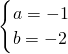 或
或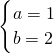 ;
;(3)
 ,因为2x>0,所以2x+1>1,
,因为2x>0,所以2x+1>1, ,
,从而
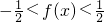 ;所以函数f(x)的值域为
;所以函数f(x)的值域为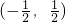 .
.分析:(1)证明不是奇函数,可用特殊值法;如证明:f(-1)≠-f(1),f(x)不是奇函数;
(2)利用奇函数定义f(-x)=-f(x),再用待定系数法求解;
(3)先将原函数式化成:
 ,将2x看成整体,利用其范围结合不等式的性质即可求得函数f(x)的值域.
,将2x看成整体,利用其范围结合不等式的性质即可求得函数f(x)的值域.点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 (a,b为实常数).
(a,b为实常数). (a,b为实常数).
(a,b为实常数). (a,b为实常数).
(a,b为实常数).