题目内容
已知⊙C1:x2+(y+5)2=5,点A(1,-3)(Ⅰ)求过点A与⊙C1相切的直线l的方程;
(Ⅱ)设⊙C2为⊙C1关于直线l对称的圆,则在x轴上是否存在点P,使得P到两圆的切线长之比为
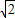 ?荐存在,求出点P的坐标;若不存在,试说明理由.
?荐存在,求出点P的坐标;若不存在,试说明理由.
【答案】分析:(Ⅰ)先判定点在圆上,用点斜式求切线l的方程.
(Ⅱ)求出对称圆的方程,设x轴上P点坐标,利用半径和PC2的距离,解出两个切线长,再用切线长之比解出结果.
解答:解:(Ⅰ)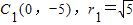 ,
,
因为点A恰在⊙C1上,所以点A即是切点,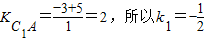 ,
,
所以,直线l的方程为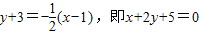 ;
;
(Ⅱ)因为点A恰为C1C2中点,所以,C2(2,-1),
所以,⊙C2:(x-2)2+(y+1)2=5,
设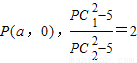 ①,或
①,或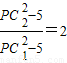 ②,
②,
由①得, ,
,
由②得,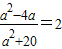 ,求此方程无解.
,求此方程无解.
综上,存在两点P(-2,0)或P(10,0)适合题意.
点评:本题(Ⅰ)A点的判定;(Ⅱ)中直角三角形的应用,对称性,弦长等知识的考查,都为本题增加了难度.
(Ⅱ)求出对称圆的方程,设x轴上P点坐标,利用半径和PC2的距离,解出两个切线长,再用切线长之比解出结果.
解答:解:(Ⅰ)
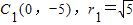 ,
,因为点A恰在⊙C1上,所以点A即是切点,
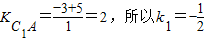 ,
,所以,直线l的方程为
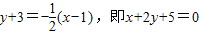 ;
;(Ⅱ)因为点A恰为C1C2中点,所以,C2(2,-1),
所以,⊙C2:(x-2)2+(y+1)2=5,
设
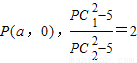 ①,或
①,或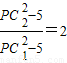 ②,
②,由①得,
 ,
,由②得,
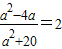 ,求此方程无解.
,求此方程无解.综上,存在两点P(-2,0)或P(10,0)适合题意.
点评:本题(Ⅰ)A点的判定;(Ⅱ)中直角三角形的应用,对称性,弦长等知识的考查,都为本题增加了难度.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知⊙C1:x2+y2+2x+8y-8=0,⊙C2:x2+y2-4x-4y-2=0,则的位置关系为( )
| A、相切 | B、相离 | C、相交 | D、内含 |